Unveiling The World: A Guide To Five Essential Map Projections

Unveiling the World: A Guide to Five Essential Map Projections

Related Articles: Unveiling the World: A Guide to Five Essential Map Projections

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Unveiling the World: A Guide to Five Essential Map Projections. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the World: A Guide to Five Essential Map Projections

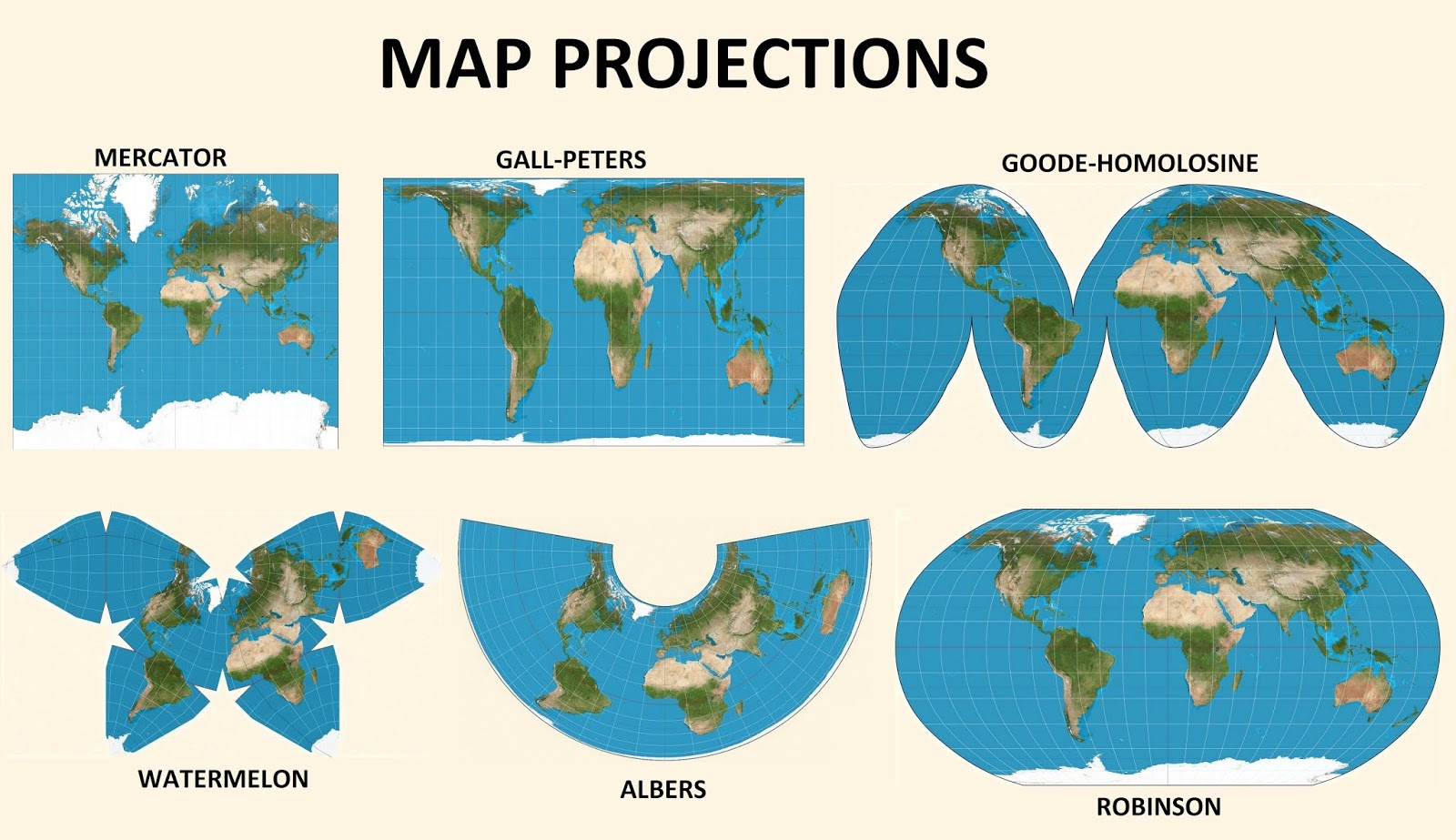
The world is a sphere, yet we perceive it as a flat surface through maps. This seemingly simple act of representation necessitates a complex process of transformation, known as map projection. Map projections are mathematical formulas that translate the Earth’s spherical surface onto a flat plane, inevitably introducing distortions in shape, size, or distance. Understanding these distortions and the strengths of different projections is crucial for interpreting geographical information accurately. This article delves into five prominent map projections, exploring their characteristics, advantages, and limitations.

1. Mercator Projection:

The Mercator projection, invented by Flemish cartographer Gerardus Mercator in 1569, remains one of the most widely recognized and utilized projections. Its defining characteristic lies in its preservation of angles, ensuring that shapes are represented accurately at all locations. This property makes the Mercator projection ideal for navigation, as compass bearings remain true across the map.

However, the Mercator projection suffers from significant distortion in areas further away from the equator. As latitude increases, landmasses are stretched, making Greenland appear larger than South America, despite the latter being significantly more extensive. This exaggeration of size at higher latitudes can lead to misinterpretations of geographical realities.

FAQs:

• What is the main purpose of the Mercator projection? The Mercator projection is primarily used for navigation due to its preservation of angles, ensuring accurate compass bearings.
• Why is the Mercator projection often criticized? The Mercator projection is criticized for its exaggeration of landmasses at higher latitudes, which can lead to misinterpretations of relative size and area.
• Are there any alternatives to the Mercator projection for navigation? Other projections, such as the Transverse Mercator or Lambert Conformal Conic, can also be used for navigation, particularly when focusing on specific regions.

Tips:

• When using a Mercator projection map, be aware of the distortion at higher latitudes and avoid drawing conclusions about the relative size of continents based on their representation.
• Consider using alternative projections for specific applications, such as the Lambert Conformal Conic for representing the contiguous United States.
• Utilize online resources and map software that allow you to switch between different projections to gain a more comprehensive understanding of geographical data.

2. Robinson Projection:

The Robinson projection, developed by Arthur H. Robinson in 1963, attempts to balance the distortions inherent in other projections by minimizing the distortion of shape, area, and distance. This compromise results in a visually appealing and relatively accurate representation of the globe.

The Robinson projection achieves its balance by using a curved grid, which reduces the stretching of landmasses at higher latitudes and minimizes the distortion of areas near the poles. However, it does not preserve angles or distances accurately, making it unsuitable for navigation.

FAQs:

• What is the primary advantage of the Robinson projection? The Robinson projection offers a balance between shape, area, and distance distortions, resulting in a visually appealing and relatively accurate representation of the globe.
• Is the Robinson projection suitable for navigation? No, the Robinson projection does not preserve angles or distances accurately, making it unsuitable for navigation.
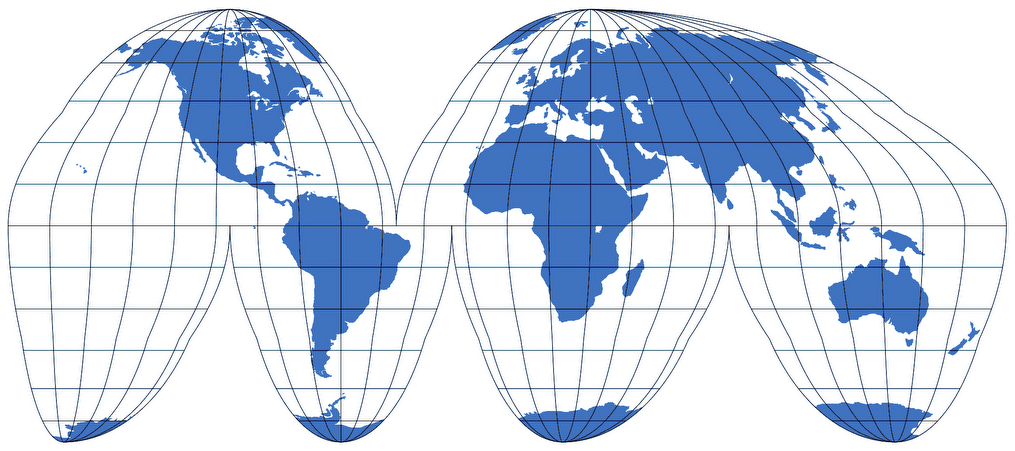
• What are some alternative projections for general-purpose mapping? Other projections, such as the Winkel Tripel and the Goode Homolosine, are also used for general-purpose mapping and offer different balances between distortions.

Tips:

• The Robinson projection is suitable for general-purpose mapping and provides a good overall representation of the globe.
• When interpreting maps based on the Robinson projection, be aware of the inherent distortions and avoid drawing conclusions about exact distances or shapes.
• Consider exploring other projections, such as the Winkel Tripel or the Goode Homolosine, to compare different approaches to minimizing distortions.

3. Gall-Peters Projection:

The Gall-Peters projection, also known as the Equal Area Projection, is a cylindrical projection that prioritizes the accurate representation of area. It maintains the relative sizes of landmasses, ensuring that continents appear in their correct proportions. This property makes the Gall-Peters projection valuable for visualizing global population distributions, resource allocation, and environmental data.

However, the Gall-Peters projection significantly distorts shapes, particularly at higher latitudes. The poles are stretched into lines, and the overall appearance of the map can be quite distorted, making it less intuitive for navigation or general-purpose mapping.

FAQs:

• What is the main purpose of the Gall-Peters projection? The Gall-Peters projection is primarily used to accurately represent the relative size of landmasses, making it valuable for visualizing global distributions and resource allocation.
• Why is the Gall-Peters projection controversial? The Gall-Peters projection is controversial due to its significant distortion of shapes, particularly at higher latitudes. Some argue that it distorts the perception of the world, while others praise its emphasis on accurately representing area.
• Are there any other projections that prioritize area preservation? Yes, other projections, such as the Mollweide projection, also prioritize area preservation and offer different visual representations of the globe.

Tips:

• Use the Gall-Peters projection when visualizing data that emphasizes relative area, such as population density or resource distribution.
• Be aware of the significant shape distortions, particularly at higher latitudes, and avoid using the Gall-Peters projection for applications that require accurate shapes.
• Consider exploring other area-preserving projections, such as the Mollweide, to compare different approaches and choose the most suitable representation for your needs.

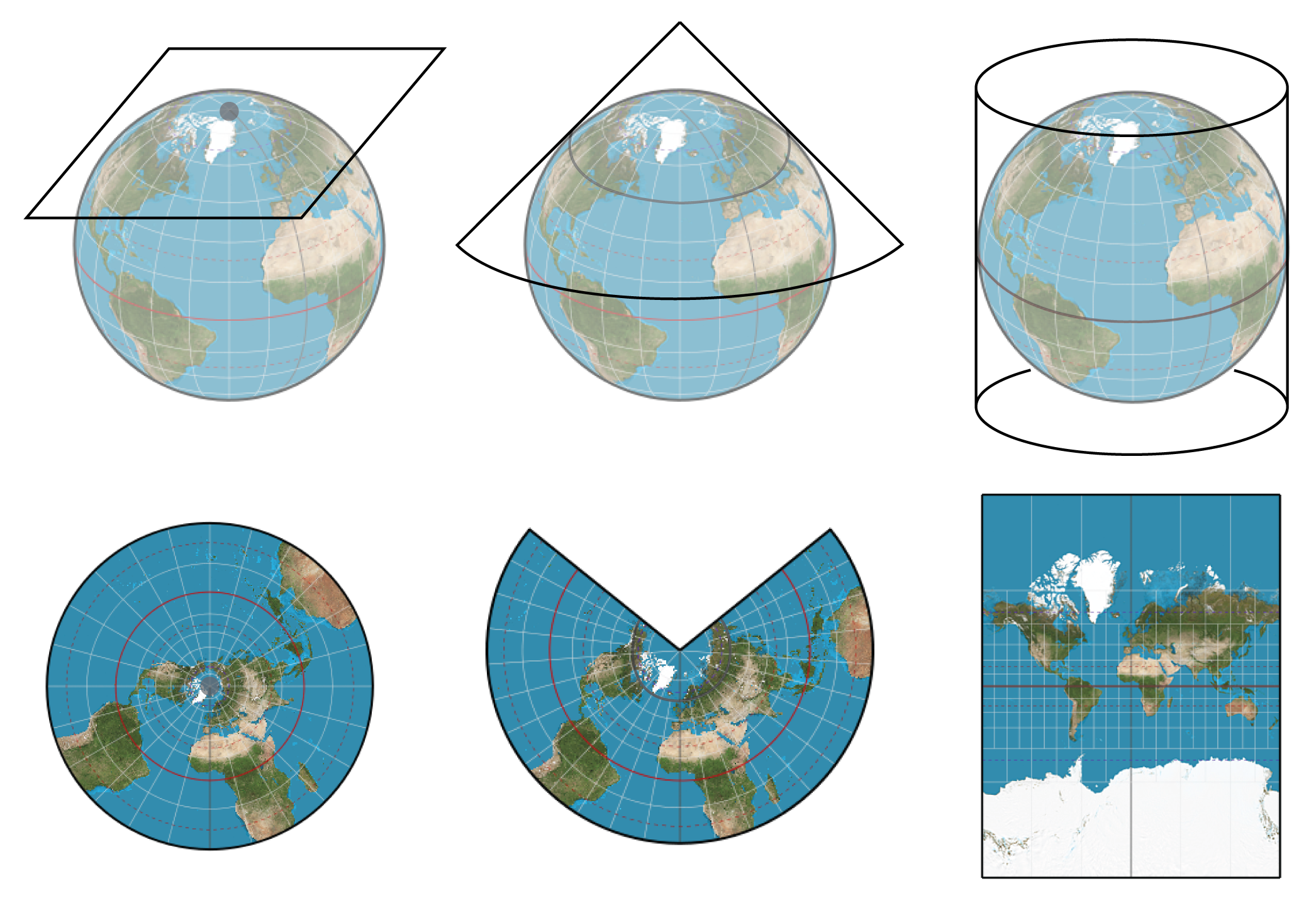
4. Lambert Conformal Conic Projection:

The Lambert Conformal Conic projection, developed by Johann Heinrich Lambert in 1772, is a conic projection that preserves angles and shapes within a specific region. This property makes it particularly suitable for mapping large areas, such as countries or continents.

The Lambert Conformal Conic projection uses a cone-shaped surface to project the Earth’s surface onto a plane. The cone intersects the globe at two standard parallels, resulting in minimal distortion within the chosen region. However, it introduces significant distortion outside the standard parallels, making it less suitable for global mapping.

FAQs:

• What is the main purpose of the Lambert Conformal Conic projection? The Lambert Conformal Conic projection is primarily used for mapping large areas, such as countries or continents, due to its preservation of angles and shapes within a specific region.
• How does the Lambert Conformal Conic projection minimize distortion? It uses a cone-shaped surface that intersects the globe at two standard parallels, minimizing distortion within the chosen region.
• What are some examples of applications for the Lambert Conformal Conic projection? The Lambert Conformal Conic projection is commonly used for mapping the contiguous United States, Canada, and other large landmasses.

Tips:

• Use the Lambert Conformal Conic projection for mapping specific regions where accurate shapes and angles are crucial.
• Choose standard parallels that best encompass the region of interest to minimize distortion within the mapped area.
• Consider using other conic projections, such as the Albers Equal Area Conic, for different applications that prioritize area preservation or other specific properties.

5. Winkel Tripel Projection:

The Winkel Tripel projection, developed by Oswald Winkel in 1921, is a compromise projection that aims to minimize distortions in both area and shape. It achieves this by combining aspects of the Mercator and Aitoff projections, resulting in a visually appealing and relatively balanced representation of the globe.

The Winkel Tripel projection is often used for general-purpose mapping, as it provides a good overall representation of the world without excessive distortion. However, it does not preserve angles or distances accurately, making it unsuitable for navigation.

FAQs:

• What is the main purpose of the Winkel Tripel projection? The Winkel Tripel projection is often used for general-purpose mapping due to its balance between area and shape distortions, resulting in a visually appealing and relatively accurate representation of the globe.
• Is the Winkel Tripel projection suitable for navigation? No, the Winkel Tripel projection does not preserve angles or distances accurately, making it unsuitable for navigation.
• What are some alternative projections for general-purpose mapping? Other projections, such as the Robinson and the Goode Homolosine, are also used for general-purpose mapping and offer different balances between distortions.

Tips:

• The Winkel Tripel projection is a good choice for general-purpose mapping when a balanced representation of the globe is desired.
• Be aware of the inherent distortions in area and shape, and avoid using the Winkel Tripel projection for applications that require accurate distances or shapes.
• Consider exploring other compromise projections, such as the Robinson or the Goode Homolosine, to compare different approaches and choose the most suitable representation for your needs.

Conclusion:

Understanding the strengths and limitations of different map projections is essential for interpreting geographical information accurately. Each projection introduces specific distortions, highlighting the inherent challenges of representing a spherical world on a flat surface. While the Mercator projection remains popular for navigation, the Robinson, Gall-Peters, Lambert Conformal Conic, and Winkel Tripel projections offer different balances between distortions, providing valuable tools for various applications, from general-purpose mapping to visualizing global data. By carefully considering the purpose and intended use of a map, users can select the most appropriate projection for their needs, ensuring accurate and insightful interpretations of geographical data.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the World: A Guide to Five Essential Map Projections. We hope you find this article informative and beneficial. See you in our next article!