Unveiling The World: A Comprehensive Guide To 10 Prominent Map Projections

Unveiling the World: A Comprehensive Guide to 10 Prominent Map Projections

Related Articles: Unveiling the World: A Comprehensive Guide to 10 Prominent Map Projections

Introduction

With great pleasure, we will explore the intriguing topic related to Unveiling the World: A Comprehensive Guide to 10 Prominent Map Projections. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the World: A Comprehensive Guide to 10 Prominent Map Projections

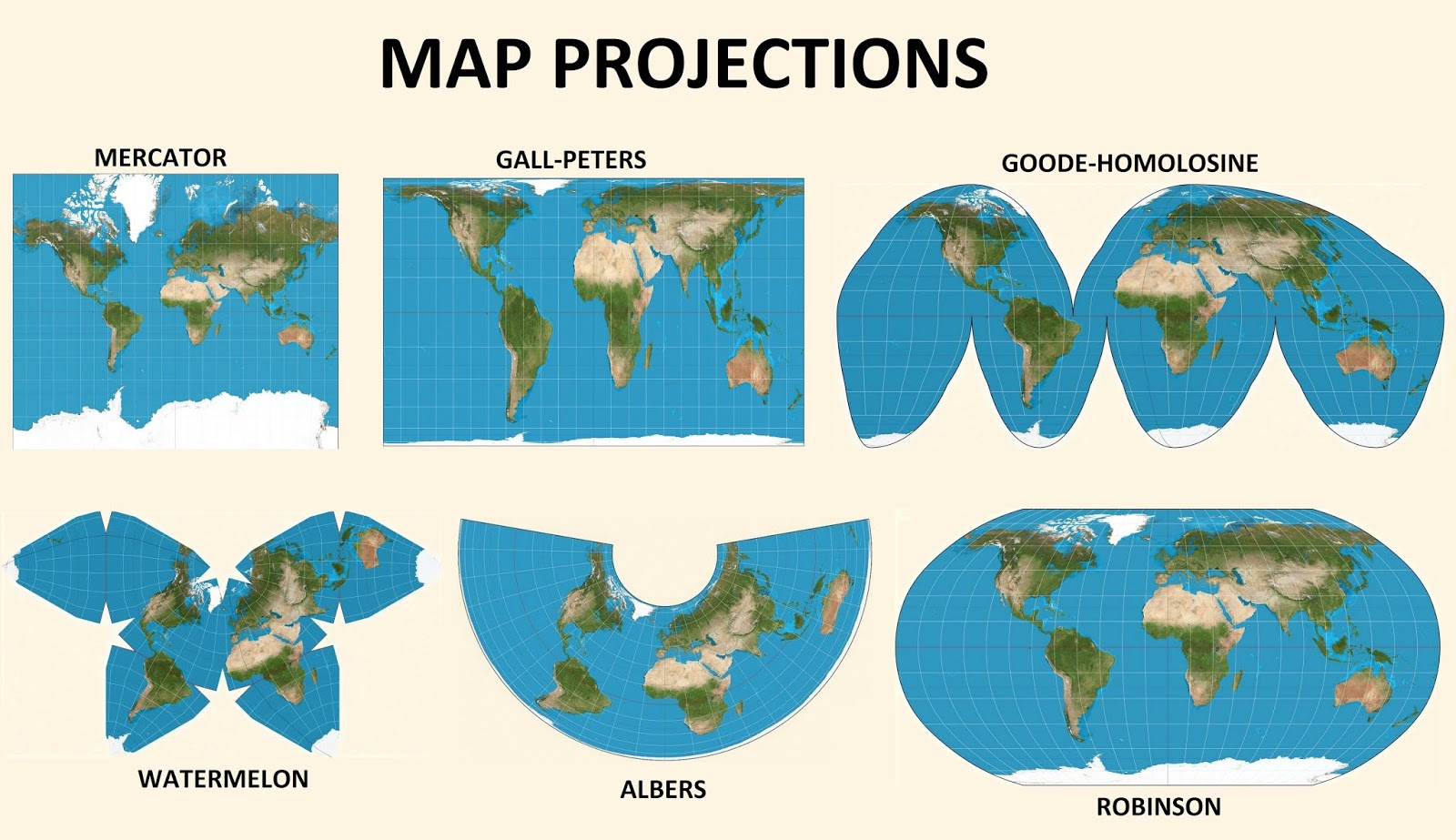
The Earth, a spherical entity, presents a unique challenge for cartographers: how to represent its curved surface on a flat map. This challenge has led to the development of numerous map projections, each with its own strengths and weaknesses. While numerous projections exist, certain ones have proven particularly valuable for specific applications, offering a balance between accuracy and visual clarity.

This article delves into ten prominent map projections, exploring their characteristics, applications, and limitations. Understanding these projections allows for a more nuanced comprehension of the world we inhabit and the ways we visualize it.

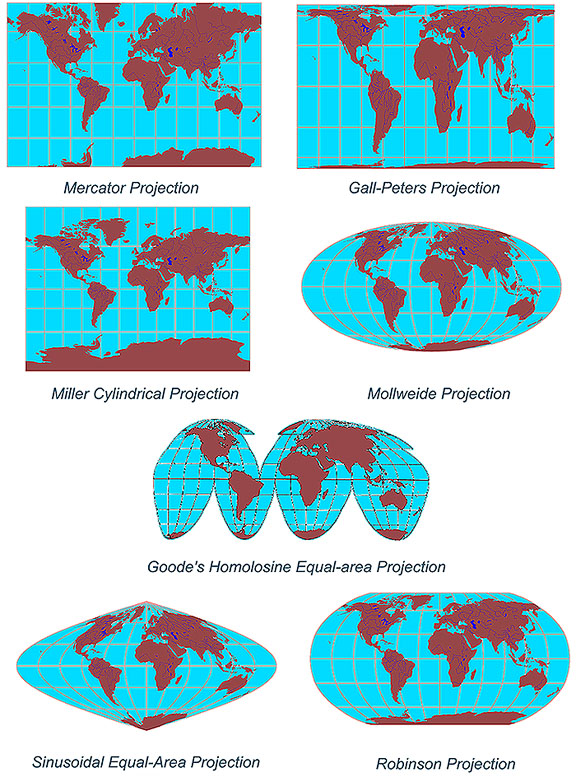
1. Mercator Projection

Developed by Flemish cartographer Gerardus Mercator in 1569, the Mercator projection remains one of the most recognizable and widely used projections. Its defining feature is its preservation of angles, making it ideal for navigation.

Characteristics:

• Conformal: Preserves angles, ensuring shapes are represented accurately, particularly at smaller scales.
• Cylindrical: Uses a cylinder wrapped around the globe as the projection surface.
• Distortion: Significant distortion of areas towards the poles, with Greenland appearing larger than South America, despite being significantly smaller in reality.

Applications:

• Navigation: Widely used in nautical charts due to its ability to represent straight lines as true compass bearings.
• Atlases and World Maps: Often used in educational settings and general reference materials.

Limitations:

• Area Distortion: Gross exaggeration of areas at higher latitudes, making it unsuitable for representing global distributions or comparisons.
• Misrepresentation of Size: Can lead to a distorted perception of the relative sizes of continents and countries.

2. Winkel Tripel Projection

Created by Oswald Winkel in 1921, the Winkel Tripel projection aims to minimize distortion in both area and shape. It achieves this by combining elements of the Mercator and Aitoff projections.

Characteristics:

• Compromise Projection: Strikes a balance between area and shape distortion.
• Equidistant: Maintains accurate distances along specific lines of longitude and latitude.
• Distortion: Moderate distortion in areas, with greater distortion at the poles.

Applications:

• World Maps: Frequently used in atlases and educational materials due to its balanced distortion.
• General Reference: Suitable for visualizing global data and trends where accurate representation of both area and shape is desired.

Limitations:

• Not Conformal: Does not preserve angles, leading to some shape distortion.
• Not Equal-Area: Does not represent areas accurately, particularly at higher latitudes.

3. Robinson Projection

Developed by Arthur H. Robinson in 1963, the Robinson projection is a compromise projection that aims to minimize distortion across the map. It achieves this by using a curved projection surface and adjusting the grid lines.

Characteristics:

• Compromise Projection: Attempts to balance area and shape distortion.
• Pseudo-Cylindrical: Uses a curved projection surface that resembles a cylinder.
• Distortion: Moderate distortion in areas and shapes, particularly at the poles.

Applications:

• World Maps: Frequently used in atlases and textbooks due to its visually appealing appearance and balanced distortion.
• General Reference: Suitable for visualizing global data and trends where a visually pleasing representation is prioritized.

Limitations:

• Not Conformal: Does not preserve angles, leading to some shape distortion.
• Not Equal-Area: Does not represent areas accurately, particularly at higher latitudes.

4. Goode Homolosine Projection

Created by John Paul Goode in 1923, the Goode Homolosine projection is an equal-area projection that uses an interrupted surface to minimize distortion. It achieves this by dividing the map into two hemispheres, with each hemisphere represented as a separate section.

Characteristics:

• Equal-Area: Preserves the relative sizes of areas, making it suitable for visualizing global distributions.
• Interrupted: Uses a discontinuous projection surface, creating gaps in the map.
• Distortion: Significant distortion in shapes, particularly at the edges of the interrupted sections.

Applications:

• World Maps: Frequently used in geographic and thematic maps to represent global data accurately.
• Climate Maps: Suitable for visualizing global climate patterns and distributions due to its preservation of area.

Limitations:

• Not Conformal: Does not preserve angles, leading to significant shape distortion.
• Interrupted Surface: Can make it challenging to visualize global connections and relationships.

5. Gall-Peters Projection

Developed by James Gall in 1855 and later popularized by Arno Peters in the 1970s, the Gall-Peters projection is an equal-area projection that aims to represent continents and countries in their true proportions.

Characteristics:

• Equal-Area: Preserves the relative sizes of areas, providing a more accurate representation of global landmasses.
• Cylindrical: Uses a cylinder wrapped around the globe as the projection surface.
• Distortion: Significant distortion in shapes, particularly at higher latitudes.

Applications:

• Social Justice Advocacy: Often used to highlight the distorted representation of developing countries in other projections.
• Thematic Maps: Suitable for visualizing global data and trends where accurate representation of areas is crucial.

Limitations:

• Not Conformal: Does not preserve angles, leading to significant shape distortion.
• Visually Distorted: Can make continents appear stretched and elongated, particularly at the equator.

6. Albers Equal-Area Conic Projection

Created by Heinrich Christian Albers in 1805, the Albers Equal-Area Conic projection is a conic projection that preserves area while minimizing distortion within a specific region.

Characteristics:

• Equal-Area: Preserves the relative sizes of areas, making it suitable for representing data within a specific region.
• Conic: Uses a cone intersecting the globe as the projection surface.
• Distortion: Moderate distortion in shapes, particularly towards the edges of the projection.

Applications:

• Regional Maps: Frequently used for mapping large countries and continents, particularly in the United States.
• Thematic Maps: Suitable for visualizing data within a specific region where accurate representation of area is important.

Limitations:

• Not Conformal: Does not preserve angles, leading to some shape distortion.
• Limited to Specific Regions: Not suitable for representing the entire globe accurately.

7. Lambert Conformal Conic Projection

Developed by Johann Heinrich Lambert in 1772, the Lambert Conformal Conic projection is a conic projection that preserves angles while minimizing distortion within a specific region.

Characteristics:

• Conformal: Preserves angles, ensuring shapes are represented accurately within a specific region.
• Conic: Uses a cone intersecting the globe as the projection surface.
• Distortion: Moderate distortion in areas, particularly towards the edges of the projection.

Applications:

• Regional Maps: Frequently used for mapping large countries and continents, particularly in the United States.
• Topographic Maps: Suitable for representing terrain features and elevations accurately within a specific region.

Limitations:

• Not Equal-Area: Does not represent areas accurately, particularly towards the edges of the projection.
• Limited to Specific Regions: Not suitable for representing the entire globe accurately.

8. Transverse Mercator Projection

A variation of the Mercator projection, the Transverse Mercator projection uses a cylinder that intersects the globe along a meridian, rather than the equator. This makes it suitable for mapping regions that are elongated along a north-south axis.

Characteristics:

• Conformal: Preserves angles, ensuring shapes are represented accurately within a specific region.
• Cylindrical: Uses a cylinder intersecting the globe along a meridian as the projection surface.
• Distortion: Significant distortion in areas and shapes, particularly towards the edges of the projection.

Applications:

• Regional Maps: Frequently used for mapping regions that are elongated along a north-south axis, such as the United Kingdom or Chile.
• Large-Scale Maps: Suitable for mapping urban areas and other regions where accurate representation of shapes is crucial.

Limitations:

• Not Equal-Area: Does not represent areas accurately, particularly towards the edges of the projection.
• Limited to Specific Regions: Not suitable for representing the entire globe accurately.

9. Stereographic Projection

The Stereographic projection is a perspective projection that uses a single point on the globe as the center of projection. This creates a circular projection that preserves angles and provides a visually appealing representation of the globe.

Characteristics:

• Conformal: Preserves angles, ensuring shapes are represented accurately.
• Perspective: Uses a single point on the globe as the center of projection.
• Distortion: Significant distortion in areas, particularly towards the edges of the projection.

Applications:

• Polar Maps: Frequently used for mapping the polar regions due to its ability to represent the entire hemisphere within a circle.
• General Reference: Suitable for visualizing the globe as a whole, particularly for educational purposes.

Limitations:

• Not Equal-Area: Does not represent areas accurately, particularly towards the edges of the projection.
• Not Suitable for Large-Scale Maps: Distortion increases significantly at larger scales.

10. Orthographic Projection

The Orthographic projection is a perspective projection that uses a point at infinity as the center of projection. This creates a projection that resembles a photograph taken from space, with a flattened appearance and a visible horizon.

Characteristics:

• Perspective: Uses a point at infinity as the center of projection.
• Distortion: Significant distortion in areas and shapes, particularly towards the edges of the projection.
• Visually Appealing: Provides a realistic representation of the globe, resembling a photograph from space.

Applications:

• Global Maps: Frequently used for visualizing the entire globe, particularly for educational purposes.
• Thematic Maps: Suitable for visualizing data that is distributed across the globe, particularly for illustrative purposes.

Limitations:

• Not Conformal: Does not preserve angles, leading to significant shape distortion.
• Not Equal-Area: Does not represent areas accurately, particularly towards the edges of the projection.

FAQs by Top 10 Map Projections

Q: What is the most accurate map projection?

A: There is no single "most accurate" map projection, as accuracy depends on the specific application and the type of distortion being minimized. Projections like the Mercator are accurate for navigation, while equal-area projections like the Goode Homolosine are more accurate for representing global distributions.

Q: Why do map projections distort the Earth?

A: The Earth is a sphere, while maps are flat. Transforming a curved surface onto a flat one inevitably involves distortion. This distortion can affect areas, shapes, distances, and angles.

Q: How do I choose the right map projection?

A: The choice of map projection depends on the purpose of the map and the type of data being represented. Consider factors such as the region being mapped, the need for accuracy in area or shape, and the visual clarity desired.

Tips by Top 10 Map Projections

• Consider the purpose of the map: What information are you trying to convey?
• Understand the strengths and weaknesses of each projection: Choose a projection that minimizes distortion in the areas and features you are interested in.
• Use multiple projections: If necessary, use different projections to represent the same data in different ways, highlighting different aspects.
• Be aware of the limitations of each projection: Do not rely on a single projection to provide a complete and accurate representation of the world.

Conclusion by Top 10 Map Projections

Map projections are essential tools for representing the Earth on a flat surface. Each projection offers a unique trade-off between accuracy and visual clarity, making it important to choose the projection that best suits the specific application. By understanding the characteristics and limitations of different projections, we can develop a more nuanced understanding of the world and the ways we visualize it.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the World: A Comprehensive Guide to 10 Prominent Map Projections. We appreciate your attention to our article. See you in our next article!