Unveiling The Power Of UMAP: A Comprehensive Guide To Dimensionality Reduction In Python

Unveiling the Power of UMAP: A Comprehensive Guide to Dimensionality Reduction in Python

Related Articles: Unveiling the Power of UMAP: A Comprehensive Guide to Dimensionality Reduction in Python

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Unveiling the Power of UMAP: A Comprehensive Guide to Dimensionality Reduction in Python. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Power of UMAP: A Comprehensive Guide to Dimensionality Reduction in Python

In the realm of data analysis, dimensionality reduction stands as a crucial technique for simplifying complex datasets and extracting meaningful insights. Among the various methods available, Uniform Manifold Approximation and Projection (UMAP) has emerged as a powerful and versatile tool, particularly within the Python ecosystem. This article delves into the intricacies of UMAP, exploring its underlying principles, practical implementation, and significant benefits.

Understanding the Essence of UMAP

UMAP is a non-linear dimensionality reduction technique that seeks to preserve the global structure of data while reducing its dimensionality. Unlike traditional methods like Principal Component Analysis (PCA), which relies on linear relationships, UMAP leverages the concept of topological data analysis to capture intricate, non-linear patterns present within high-dimensional datasets.

The Mechanics of UMAP

At its core, UMAP operates in two distinct phases:

1. Construction of a Neighborhood Graph: UMAP begins by constructing a nearest neighbor graph that captures the local structure of the data. This graph represents the relationships between data points, highlighting those that are close to each other in the high-dimensional space.

2. Projection onto a Lower-Dimensional Space: The constructed neighborhood graph serves as the foundation for projecting the data onto a lower-dimensional space. UMAP employs a sophisticated optimization algorithm that minimizes the difference between the distances in the high-dimensional space and the projected space. This optimization process ensures that the global structure of the data is preserved as effectively as possible.

Implementing UMAP in Python

The implementation of UMAP in Python is made remarkably straightforward thanks to the dedicated umap library. This library provides a user-friendly interface for applying UMAP to a wide range of data types, including numerical arrays, pandas DataFrames, and scikit-learn datasets.

A Practical Example

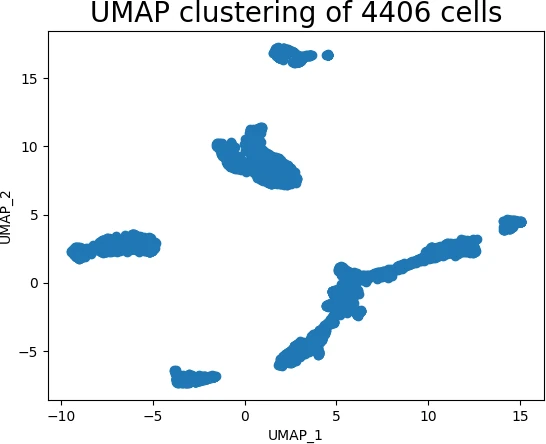
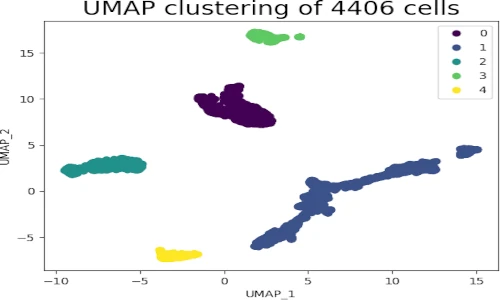
Let’s consider a hypothetical scenario where we have a dataset representing customer purchase history. Each data point corresponds to a customer, and the features represent their purchase frequency, average purchase value, and preferred product categories. Our goal is to visualize the customer base and identify clusters of customers with similar buying patterns.

import umap
import pandas as pd

# Load the customer data
data = pd.read_csv('customer_data.csv')

# Extract relevant features
features = data[['purchase_frequency', 'average_purchase_value', 'preferred_category']]

# Initialize and fit the UMAP model
reducer = umap.UMAP(n_components=2, random_state=42)
embedding = reducer.fit_transform(features)

# Visualize the embedded data
import matplotlib.pyplot as plt
plt.scatter(embedding[:, 0], embedding[:, 1])
plt.xlabel('UMAP Dimension 1')
plt.ylabel('UMAP Dimension 2')
plt.title('Customer Base Visualization')
plt.show()

In this example, we first import the necessary libraries, load the customer data, and select the relevant features. We then initialize a UMAP model with two components (for visualization purposes) and fit it to the data. The fit_transform method performs both the fitting and embedding steps, resulting in a 2D representation of the customer data. Finally, we visualize the embedded data using a scatter plot, revealing potential clusters of customers with similar buying patterns.

Advantages of UMAP

The adoption of UMAP has been fueled by its numerous advantages over traditional dimensionality reduction techniques:

• Preservation of Global Structure: UMAP excels at preserving the global structure of the data, ensuring that points that are close in the high-dimensional space remain close in the reduced space. This is crucial for maintaining the integrity of the data and enabling meaningful insights.

• Handling Non-linear Relationships: Unlike linear methods like PCA, UMAP effectively captures non-linear relationships between data points, allowing for more accurate representations of complex datasets.

• Scalability and Efficiency: UMAP is designed to handle large datasets efficiently, making it suitable for real-world applications involving substantial amounts of data.

• Interpretability: The embedded representation generated by UMAP is often more interpretable than those produced by other techniques, facilitating easier analysis and visualization.

Addressing Common Questions

Q: What are the key parameters to adjust in UMAP?

A: The umap library offers a range of parameters that can be customized to fine-tune the model’s behavior. Some of the most important parameters include:

• n_components: Specifies the number of dimensions in the reduced space.
• n_neighbors: Controls the size of the local neighborhood used for constructing the neighborhood graph.
• min_dist: Influences the degree of separation between points in the embedded space.
• metric: Determines the distance metric used for calculating distances between data points.

Q: How can I evaluate the performance of UMAP?

A: Evaluating the performance of UMAP involves assessing how well it preserves the structure of the original data in the reduced space. Common evaluation metrics include:

• Neighborhood Preservation: Measures how well the local neighborhood structure is preserved in the embedding.
• Global Structure Preservation: Assesses the overall preservation of the global structure of the data.
• Visual Inspection: Examining the embedded data visually to assess the quality of the representation.

Q: What are some best practices for using UMAP?

A: To maximize the effectiveness of UMAP, consider the following best practices:

• Data Preprocessing: Ensure that the data is properly preprocessed before applying UMAP. This may involve scaling, normalization, or handling missing values.

• Parameter Tuning: Experiment with different parameter settings to find the optimal configuration for your specific dataset.

• Visual Inspection: Always visually inspect the embedded data to ensure that it accurately reflects the underlying structure of the original data.

Conclusion

UMAP has emerged as a powerful and versatile dimensionality reduction technique, offering a compelling alternative to traditional methods. Its ability to capture non-linear relationships, preserve global structure, and handle large datasets efficiently makes it a valuable tool for data analysis across various domains. By leveraging its capabilities, researchers and practitioners can gain deeper insights from complex datasets, unlock hidden patterns, and drive informed decision-making.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Power of UMAP: A Comprehensive Guide to Dimensionality Reduction in Python. We appreciate your attention to our article. See you in our next article!