Unveiling the Power of the Lambert Conformal Conic Projection: A Comprehensive Guide
Related Articles: Unveiling the Power of the Lambert Conformal Conic Projection: A Comprehensive Guide
Introduction
In this auspicious occasion, we are delighted to delve into the intriguing topic related to Unveiling the Power of the Lambert Conformal Conic Projection: A Comprehensive Guide. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
Unveiling the Power of the Lambert Conformal Conic Projection: A Comprehensive Guide
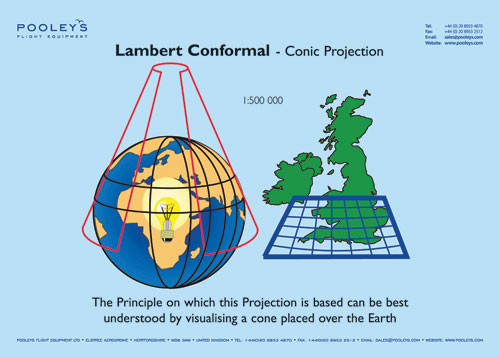
The world is a sphere, but our maps are flat. This fundamental discrepancy necessitates the use of map projections, mathematical transformations that translate the Earth’s curved surface onto a two-dimensional plane. Among the myriad projections available, the Lambert Conformal Conic projection stands out for its remarkable accuracy and versatility, particularly for representing regions with significant north-south extent.
Understanding the Fundamentals
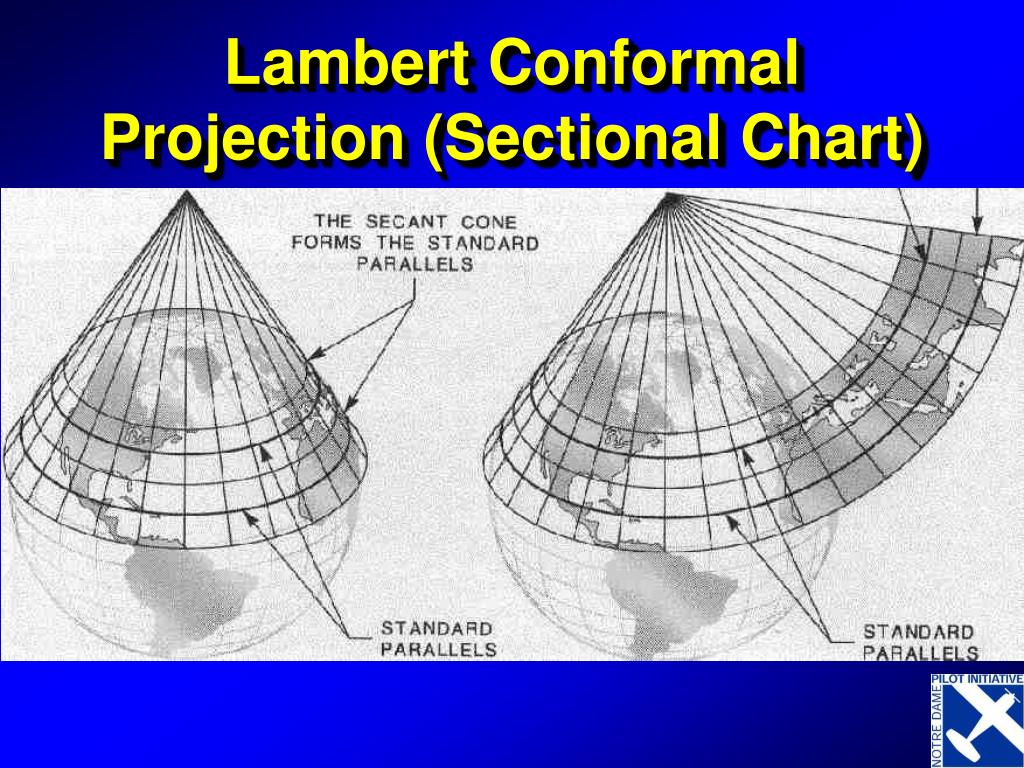
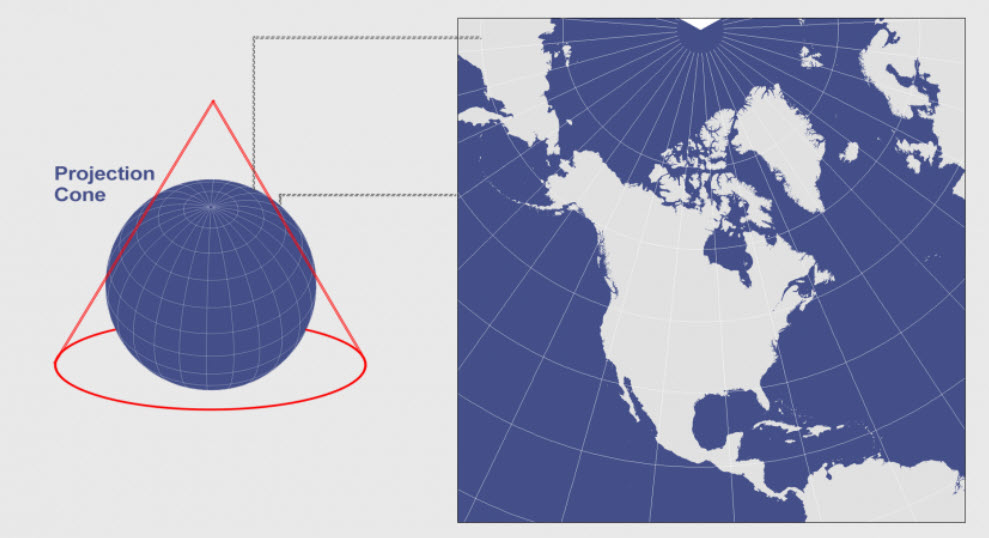
The Lambert Conformal Conic projection, often simply referred to as the Lambert projection, belongs to the family of conic projections. Conic projections visualize the Earth as if a cone were wrapped around it, with the cone’s apex positioned above a specific point on the globe. The projection then unfolds the cone, creating a flat map.
Key Features and Advantages
The defining characteristic of the Lambert projection lies in its conformal nature. This means that it preserves angles at any point on the map. This property is crucial for applications requiring accurate representation of shapes and directions, such as navigation and surveying.
Several advantages make the Lambert projection a popular choice for cartographers and spatial analysts:
-
Minimal Distortion: While no projection can perfectly represent a sphere on a flat surface, the Lambert projection minimizes distortion, especially within a designated central meridian. This is particularly beneficial for representing regions that extend predominantly north-south, where other projections might introduce significant shape distortions.
-
Preservation of Shape and Direction: The conformal nature of the Lambert projection ensures that shapes and directions are accurately represented, particularly within the central meridian zone. This makes it ideal for applications requiring precise measurements and analysis of geographical features.
-
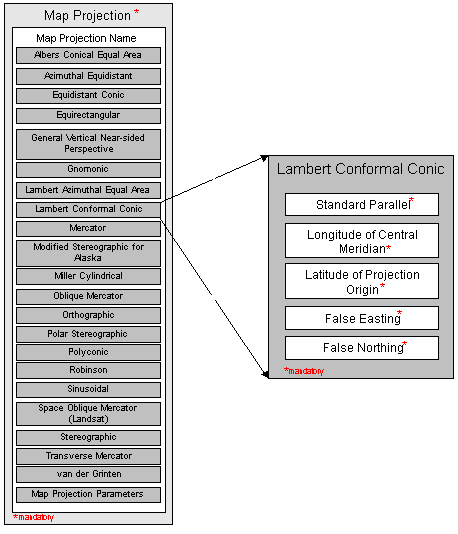
Flexibility and Customization: The Lambert projection allows for customization by adjusting its parameters. This includes the choice of standard parallels (lines of latitude that define the cone’s intersection with the sphere) and the central meridian. This flexibility enables the creation of projections tailored to specific geographic areas and desired levels of accuracy.
Applications and Importance
The Lambert projection finds widespread application in various fields due to its accuracy and versatility:
-
Mapping and Cartography: The Lambert projection is commonly used for creating maps of countries and regions, particularly those with significant north-south extent. It is a standard projection for topographic maps, atlases, and geographical information systems (GIS).
-
Navigation and Surveying: The accurate representation of angles and shapes makes the Lambert projection ideal for navigation and surveying applications. It is used in aeronautical charts, nautical charts, and land surveying to ensure precise measurements and directions.
-
Weather Forecasting: Meteorological data, often presented on maps, relies heavily on accurate representation of geographical features and distances. The Lambert projection’s ability to preserve shape and minimize distortion makes it a valuable tool for weather forecasting and analysis.
-
Environmental Monitoring: Environmental studies often involve analyzing spatial data, such as air pollution levels, deforestation patterns, and wildlife distribution. The Lambert projection’s accuracy and flexibility make it a preferred choice for environmental monitoring and mapping.
Common Lambert Projections
The Lambert Conformal Conic projection is further categorized into specific types, each optimized for specific applications:
-
Lambert Conformal Conic Projection (LCC): The standard Lambert projection, widely used for mapping and surveying purposes.
-
Lambert Conformal Conic Projection, 1SP: A variation of the LCC projection with a single standard parallel, simplifying calculations and making it suitable for smaller geographic areas.
-
Lambert Conformal Conic Projection, 2SP: The most common type of Lambert projection, using two standard parallels to minimize distortion across a wider area.
Frequently Asked Questions
Q: What are the limitations of the Lambert Conformal Conic projection?
A: Despite its advantages, the Lambert projection is not without limitations. It introduces significant distortion in areas far from the central meridian. This means that areas near the edges of the projected region may appear stretched or compressed. Additionally, the Lambert projection is not suitable for representing the entire globe, as distortion increases with distance from the central meridian.
Q: How do I choose the appropriate Lambert projection for my needs?
A: The choice of Lambert projection depends on the specific geographic area and the level of accuracy required. For smaller regions, a 1SP Lambert projection might suffice. For larger areas, a 2SP Lambert projection is often preferred. The standard parallels and the central meridian should be carefully selected to minimize distortion within the area of interest.
Q: What are some alternative map projections to the Lambert projection?
A: While the Lambert projection is a powerful tool, other map projections are available for specific needs. These include:
-
Mercator Projection: Preserves angles and directions but distorts areas near the poles.
-
Transverse Mercator Projection: Minimizes distortion along a central meridian, ideal for mapping regions with significant east-west extent.
-
Albers Equal-Area Conic Projection: Preserves areas but distorts shapes.
Tips for Using the Lambert Projection
-
Understanding the Distortion: Be aware of the limitations of the Lambert projection, particularly the distortion that occurs away from the central meridian.
-
Choosing the Right Parameters: Carefully select the standard parallels and central meridian to minimize distortion within the area of interest.
-
Using Geographic Information Systems (GIS): GIS software provides powerful tools for working with map projections, including the Lambert projection.
Conclusion
The Lambert Conformal Conic projection stands as a testament to the ingenuity of cartographers and mathematicians. Its ability to accurately represent shapes and directions, especially within a central meridian zone, makes it an invaluable tool for mapping, navigation, surveying, and various other applications. While no projection can completely eliminate distortion, the Lambert projection offers a compelling balance between accuracy and practicality, making it a cornerstone of spatial analysis and representation. By understanding its principles and limitations, users can leverage its power to accurately depict the world around us.




Closure
Thus, we hope this article has provided valuable insights into Unveiling the Power of the Lambert Conformal Conic Projection: A Comprehensive Guide. We appreciate your attention to our article. See you in our next article!
