Unveiling The Power Of Dimensionality Reduction: A Comprehensive Guide To UMAP In Python

Unveiling the Power of Dimensionality Reduction: A Comprehensive Guide to UMAP in Python

Related Articles: Unveiling the Power of Dimensionality Reduction: A Comprehensive Guide to UMAP in Python

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Unveiling the Power of Dimensionality Reduction: A Comprehensive Guide to UMAP in Python. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Power of Dimensionality Reduction: A Comprehensive Guide to UMAP in Python

In the realm of data analysis, the ability to effectively visualize high-dimensional datasets is paramount. However, the human mind struggles to comprehend data with more than three dimensions. This is where dimensionality reduction techniques come into play, offering a powerful solution to transform high-dimensional data into lower-dimensional representations while preserving its inherent structure. Among these techniques, Uniform Manifold Approximation and Projection (UMAP) has emerged as a robust and versatile tool, particularly in the Python ecosystem.

This article provides a comprehensive exploration of UMAP in Python, delving into its core principles, implementation, and practical applications. We will examine how UMAP excels in capturing the underlying manifold structure of data, enabling insightful visualizations and facilitating downstream analysis.

Understanding the Essence of UMAP

UMAP is a non-linear dimensionality reduction technique rooted in the concept of manifold learning. It assumes that high-dimensional data points lie on a lower-dimensional manifold embedded in the high-dimensional space. UMAP aims to discover this underlying manifold and project the data onto it, effectively reducing dimensionality while preserving the topological structure and local neighborhood relationships.

Key Features of UMAP:

• Preservation of Global and Local Structure: UMAP prioritizes the preservation of both the global and local structure of the data. This ensures that the relationships between data points are accurately reflected in the reduced space, making it ideal for visualizing complex datasets.
• Robustness to Noise and Outliers: UMAP exhibits robustness to noise and outliers, making it suitable for real-world datasets that often contain imperfections.
• Scalability and Efficiency: UMAP is designed to handle large datasets efficiently, making it a practical choice for real-world applications.
• Hyperparameter Tuning: UMAP provides a set of hyperparameters that can be adjusted to fine-tune the dimensionality reduction process, allowing for customization based on specific data characteristics.

Implementing UMAP in Python

The Python implementation of UMAP is provided by the umap-learn library, which offers a user-friendly interface for applying UMAP to various datasets. Let’s explore a step-by-step guide to implementing UMAP in Python:

1. Installation:

pip install umap-learn

2. Importing the Library:

import umap

3. Loading and Preprocessing Data:

import pandas as pd
from sklearn.datasets import load_iris

# Load the Iris dataset
iris = load_iris()
data = iris.data
labels = iris.target

# Create a pandas DataFrame for easier manipulation
df = pd.DataFrame(data, columns=iris.feature_names)

4. Creating the UMAP Model:

# Initialize a UMAP model with desired parameters
reducer = umap.UMAP(n_components=2, random_state=42)

5. Fitting the Model:

# Fit the UMAP model to the data
embedding = reducer.fit_transform(data)

6. Visualizing the Reduced Data:

import matplotlib.pyplot as plt

# Create a scatter plot of the reduced data
plt.scatter(embedding[:, 0], embedding[:, 1], c=labels)
plt.xlabel('UMAP Dimension 1')
plt.ylabel('UMAP Dimension 2')
plt.title('UMAP Embedding of Iris Dataset')
plt.show()

Understanding Hyperparameters:

• n_components: The number of dimensions to reduce the data to.
• n_neighbors: The number of nearest neighbors to consider for each data point.
• min_dist: The minimum distance between points in the reduced space.
• metric: The distance metric used for calculating nearest neighbors.
• random_state: Controls the random number generator for reproducibility.

Illustrative Applications of UMAP:

• Visualizing High-Dimensional Datasets: UMAP excels at visualizing complex datasets, revealing hidden structures and patterns that are not apparent in the original high-dimensional space. This is particularly useful in fields like image analysis, genomics, and machine learning.
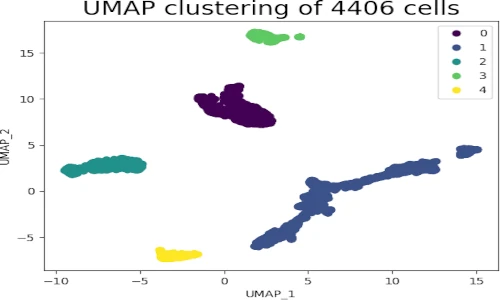
• Clustering and Anomaly Detection: UMAP can facilitate clustering and anomaly detection by preserving the local neighborhood structure of the data. The reduced representation allows for easier identification of clusters and outliers.
• Feature Engineering: UMAP can be used as a feature engineering technique to create new features from existing ones. The reduced dimensions can capture important information and serve as input for downstream machine learning models.
• Data Exploration and Analysis: UMAP provides a powerful tool for exploring and understanding data, allowing researchers to gain insights into the underlying relationships and patterns within complex datasets.

Addressing Common Queries: A Comprehensive FAQ

Q1: What are the advantages of UMAP over other dimensionality reduction techniques like PCA?

A1: UMAP offers several advantages over PCA:

• Non-Linearity: UMAP can capture non-linear relationships in the data, while PCA is limited to linear relationships.
• Preservation of Local Structure: UMAP excels at preserving the local neighborhood structure of the data, which is crucial for tasks like clustering and anomaly detection.
• Robustness to Noise: UMAP is more robust to noise and outliers than PCA.

Q2: How do I choose the optimal hyperparameters for UMAP?

A2: Choosing the optimal hyperparameters for UMAP often involves experimentation and domain knowledge. Here are some guidelines:

• n_neighbors: Start with a value between 5 and 50, depending on the size and density of the data.
• min_dist: This parameter controls the crowding of points in the reduced space. Experiment with values between 0 and 1.
• metric: The choice of metric depends on the nature of the data. Euclidean distance is a common choice for continuous data, while Manhattan distance is suitable for categorical data.

Q3: Can UMAP be used for both supervised and unsupervised learning?

A3: UMAP is primarily an unsupervised learning technique. However, it can be integrated into supervised learning tasks by using the reduced representation as input for a supervised model.

Q4: What are the limitations of UMAP?

A4: While UMAP is a powerful technique, it does have some limitations:

• Computational Cost: UMAP can be computationally expensive for very large datasets.
• Interpretability: The reduced dimensions may not always be easily interpretable, making it challenging to understand the underlying relationships in the data.

Enhancing UMAP Implementation: Valuable Tips

• Data Scaling: Scaling the data before applying UMAP can improve its performance.
• Hyperparameter Tuning: Utilize techniques like grid search or random search to find the optimal hyperparameters for your specific dataset.
• Visualization: Visualize the reduced data using scatter plots, histograms, or other appropriate methods to gain insights into the underlying structure.
• Dimensionality Selection: Experiment with different numbers of dimensions to find the optimal balance between dimensionality reduction and preservation of data structure.

Conclusion: A Powerful Tool for Data Exploration and Analysis

UMAP has emerged as a powerful tool for dimensionality reduction, offering a unique blend of non-linearity, preservation of local structure, and robustness to noise. Its Python implementation provides a user-friendly interface for applying UMAP to diverse datasets, enabling insightful visualizations, facilitating clustering and anomaly detection, and enhancing downstream analysis. As the field of data analysis continues to evolve, UMAP is poised to play an increasingly vital role in unlocking the hidden insights within complex datasets, paving the way for more informed decision-making and deeper understanding of the world around us.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Power of Dimensionality Reduction: A Comprehensive Guide to UMAP in Python. We thank you for taking the time to read this article. See you in our next article!