Unveiling the Power of Dimensionality Reduction: A Comprehensive Guide to UMAP in Python
Related Articles: Unveiling the Power of Dimensionality Reduction: A Comprehensive Guide to UMAP in Python
Introduction
In this auspicious occasion, we are delighted to delve into the intriguing topic related to Unveiling the Power of Dimensionality Reduction: A Comprehensive Guide to UMAP in Python. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
Unveiling the Power of Dimensionality Reduction: A Comprehensive Guide to UMAP in Python

In the realm of data science, the ability to effectively visualize and analyze high-dimensional datasets is paramount. However, the human mind struggles to grasp data beyond three dimensions, making direct visualization challenging. This is where dimensionality reduction techniques come into play. Among these, Uniform Manifold Approximation and Projection (UMAP) has emerged as a powerful and versatile tool for navigating the complex landscape of high-dimensional data.
Understanding the Essence of UMAP
UMAP is a non-linear dimensionality reduction algorithm that aims to preserve the global structure of data while projecting it into a lower-dimensional space. It operates on the fundamental principle that high-dimensional data often lies on a lower-dimensional manifold, a geometric object embedded in the higher-dimensional space. UMAP seeks to uncover this underlying manifold and represent the data points in a lower-dimensional space that captures the essential relationships between them.
Key Features and Advantages of UMAP
- Preservation of Local and Global Structure: UMAP excels at preserving both the local and global relationships between data points. This means that clusters and neighborhoods are maintained in the reduced space, while the overall structure of the data is also faithfully represented.
- Speed and Efficiency: Compared to other dimensionality reduction techniques like t-SNE, UMAP is significantly faster, particularly for large datasets. This efficiency makes it suitable for real-time analysis and interactive exploration of data.
- Robustness to Noise and Outliers: UMAP demonstrates robustness to noise and outliers, making it a reliable choice for handling real-world data that often contains imperfections.
- Flexibility and Customization: UMAP offers a range of parameters that can be adjusted to fine-tune the reduction process, allowing for tailored results depending on the specific data and analysis goals.
Implementation of UMAP in Python
The UMAP algorithm is readily available in Python through the umap library. This library provides a user-friendly interface for applying UMAP to various data analysis tasks.
Example: Visualizing MNIST Handwritten Digits
Consider the MNIST dataset, a collection of handwritten digits. Each digit is represented by a 784-dimensional vector, making it challenging to visualize directly. UMAP can be used to project this data into a 2D space, revealing the underlying structure of the dataset:
import umap
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
# Load MNIST dataset
digits = load_digits()
X = digits.data
y = digits.target
# Create UMAP object
reducer = umap.UMAP(n_components=2, random_state=42)
# Fit UMAP to data
embedding = reducer.fit_transform(X)
# Visualize the embedding
plt.figure(figsize=(10, 6))
plt.scatter(embedding[:, 0], embedding[:, 1], c=y, cmap='viridis')
plt.title('UMAP Embedding of MNIST Digits')
plt.xlabel('UMAP Dimension 1')
plt.ylabel('UMAP Dimension 2')
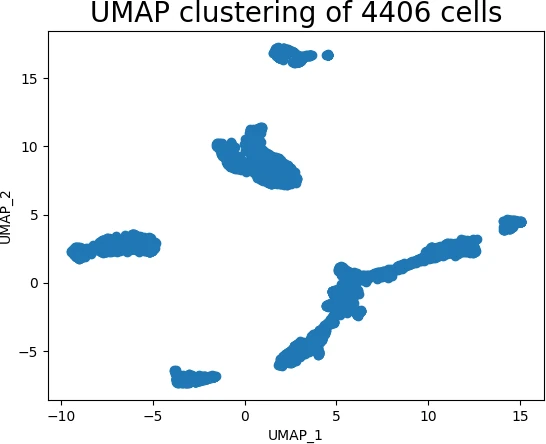
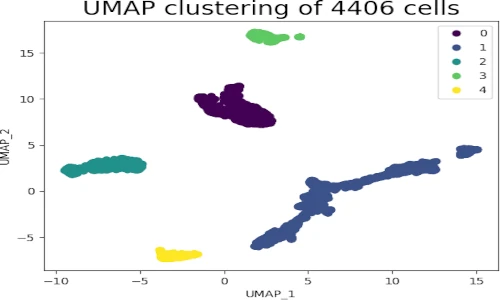
plt.show()This code snippet demonstrates the ease of applying UMAP to a real-world dataset. The resulting plot reveals clusters of points corresponding to different digits, showcasing the ability of UMAP to preserve the underlying structure of the data.
Beyond Visualization: Applications of UMAP
UMAP’s capabilities extend far beyond visualization. It finds applications in various domains, including:
- Clustering and Anomaly Detection: UMAP’s ability to preserve local structure makes it effective for identifying clusters and detecting outliers in high-dimensional datasets.
- Data Exploration and Discovery: UMAP enables researchers to explore complex datasets and discover hidden relationships between variables.
- Machine Learning: UMAP can be used as a preprocessing step for machine learning models, reducing the dimensionality of input features and improving model performance.
- Natural Language Processing: UMAP finds applications in natural language processing, where it can be used to represent text data in a lower-dimensional space, facilitating tasks like text classification and sentiment analysis.
FAQs on UMAP in Python
Q: What are the key parameters to adjust in UMAP?
A: UMAP offers several parameters that can be adjusted to fine-tune the reduction process. Some key parameters include:
- n_neighbors: This parameter determines the local neighborhood size used for constructing the manifold. A higher value leads to a broader view of the data, while a lower value focuses on local relationships.
- min_dist: This parameter controls the minimum distance between points in the reduced space. A higher value results in more spread-out points, while a lower value leads to more tightly clustered points.
- metric: This parameter specifies the distance metric used for calculating distances between data points. Different metrics can lead to varying results depending on the nature of the data.
Q: How does UMAP compare to other dimensionality reduction techniques like t-SNE?
A: While both UMAP and t-SNE are effective dimensionality reduction techniques, they have different strengths and weaknesses:
- Speed: UMAP is generally faster than t-SNE, particularly for large datasets.
- Global Structure: UMAP excels at preserving both local and global structure, while t-SNE may struggle to preserve global relationships.
- Robustness: UMAP is more robust to noise and outliers than t-SNE.
Q: How can I optimize UMAP parameters for my specific dataset?
A: Optimizing UMAP parameters involves understanding the nature of your data and the specific goals of your analysis. Experimenting with different parameter combinations is crucial. Techniques like grid search and cross-validation can be employed to find the optimal parameter settings for your dataset.
Tips for Effective UMAP Usage
- Data Preprocessing: Before applying UMAP, it is often beneficial to preprocess the data by scaling or standardizing features. This can improve the performance of the algorithm.
- Parameter Tuning: Experiment with different parameter settings to find the best configuration for your data.
- Visualization and Interpretation: Visualize the reduced data to gain insights into the underlying structure. Use tools like scatter plots and heatmaps to explore the relationships between variables.
- Combine with Other Techniques: UMAP can be used in conjunction with other techniques, such as clustering or classification algorithms, to enhance the analysis process.
Conclusion: UMAP as a Powerful Tool for Data Exploration
UMAP has emerged as a powerful and versatile tool for dimensionality reduction, enabling researchers and data scientists to effectively visualize and analyze high-dimensional datasets. Its ability to preserve both local and global structure, coupled with its speed and robustness, makes it a valuable asset for various data analysis tasks. By understanding the principles behind UMAP and its implementation in Python, users can unlock its potential to explore complex data, discover hidden relationships, and gain deeper insights into the underlying patterns within their data.






Closure
Thus, we hope this article has provided valuable insights into Unveiling the Power of Dimensionality Reduction: A Comprehensive Guide to UMAP in Python. We appreciate your attention to our article. See you in our next article!