Unveiling The Power Of Dimensionality Reduction: A Comprehensive Exploration Of The UMAP Python Package

Unveiling the Power of Dimensionality Reduction: A Comprehensive Exploration of the UMAP Python Package

Related Articles: Unveiling the Power of Dimensionality Reduction: A Comprehensive Exploration of the UMAP Python Package

Introduction

With great pleasure, we will explore the intriguing topic related to Unveiling the Power of Dimensionality Reduction: A Comprehensive Exploration of the UMAP Python Package. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Power of Dimensionality Reduction: A Comprehensive Exploration of the UMAP Python Package

In the realm of data analysis, the curse of dimensionality presents a formidable challenge. As the number of features in a dataset grows, it becomes increasingly difficult to visualize and understand the underlying patterns and relationships. Dimensionality reduction techniques offer a solution by transforming high-dimensional data into a lower-dimensional representation, preserving essential information while simplifying analysis. Among these techniques, the Uniform Manifold Approximation and Projection (UMAP) method stands out as a powerful and versatile tool, readily accessible through the UMAP Python package.

Understanding the Essence of UMAP

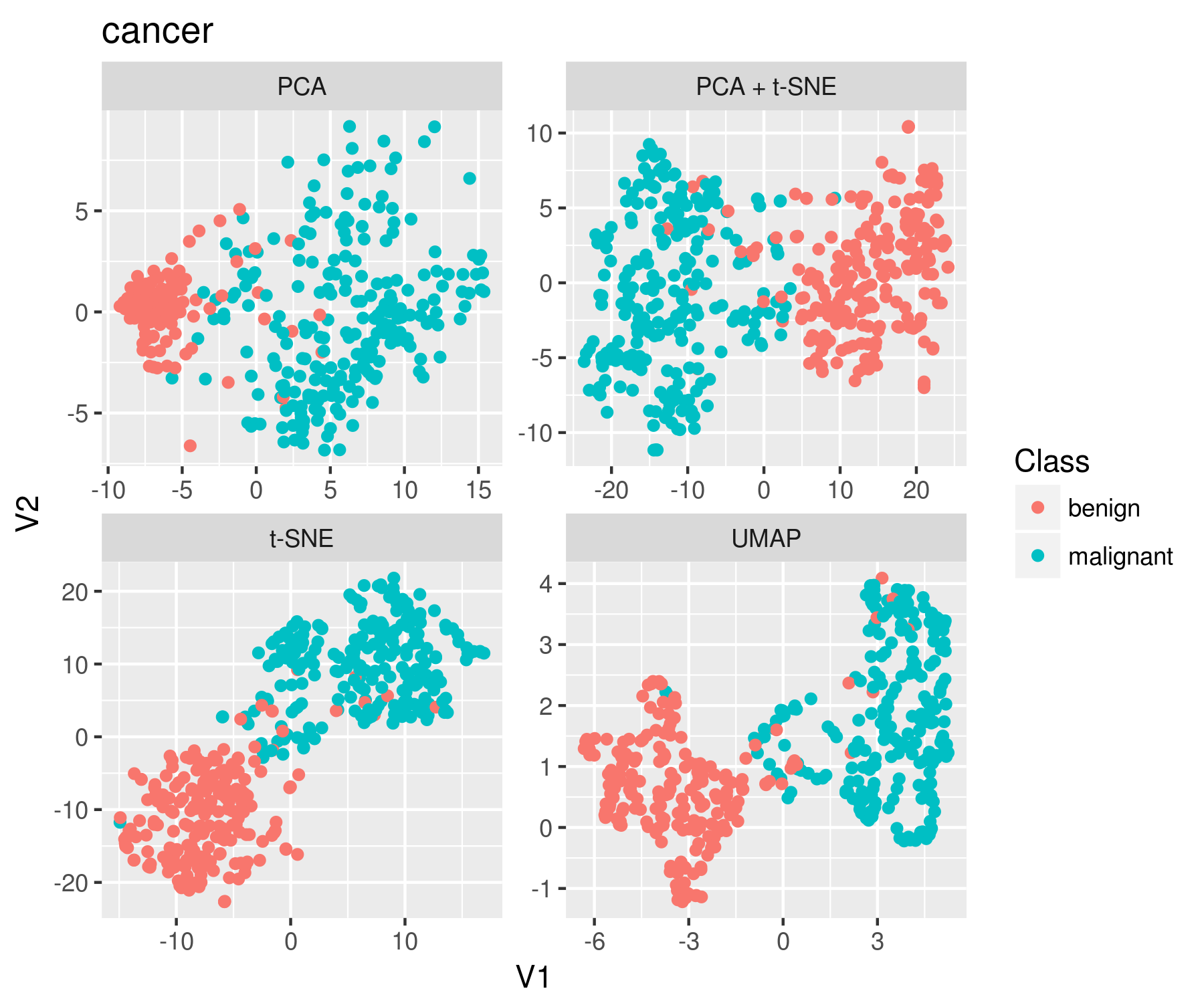
UMAP is a non-linear dimensionality reduction technique that excels at preserving the global structure of data, even in high-dimensional spaces. Unlike traditional methods like Principal Component Analysis (PCA), which primarily focus on linear relationships, UMAP leverages the concept of topological data analysis to capture complex, non-linear structures. This makes it particularly well-suited for datasets where intricate relationships exist between data points.

At its core, UMAP operates by constructing a simplified representation of the data’s underlying manifold, a continuous space that captures the inherent relationships between data points. This manifold is approximated using a graph-based approach, where each data point is connected to its nearest neighbors, forming a network. The algorithm then optimizes the embedding of these points in a lower-dimensional space while preserving the topological structure of the original manifold.

Key Features and Benefits of UMAP

The UMAP Python package provides a robust and user-friendly implementation of the UMAP algorithm, offering numerous features and benefits for data analysis:

• Preservation of Global Structure: UMAP excels at preserving the global structure of data, enabling the visualization of complex, non-linear relationships that might be obscured in high-dimensional space.
• Scalability: The algorithm is designed to handle large datasets efficiently, making it suitable for real-world applications involving massive amounts of data.
• Interpretability: UMAP provides interpretable results, allowing researchers to understand the underlying structure of the data and identify meaningful clusters or patterns.
• Flexibility: The package offers a wide range of customization options, allowing users to fine-tune parameters such as the number of neighbors, the dimensionality of the embedding space, and the metric used to measure distances between data points.
• Visualization Capabilities: UMAP integrates seamlessly with popular visualization libraries like Matplotlib and Seaborn, enabling the creation of insightful plots that reveal the structure of the reduced data.

Practical Applications of UMAP

The versatility of UMAP makes it a valuable tool in various domains, including:

• Machine Learning: UMAP is often employed as a preprocessing step for machine learning algorithms, reducing the dimensionality of data while preserving important features.
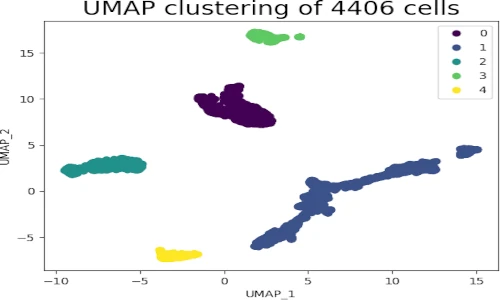
• Data Exploration and Visualization: It facilitates the exploration and visualization of high-dimensional data, revealing hidden patterns and structures that might be missed using traditional methods.
• Bioinformatics: UMAP is widely used in bioinformatics for analyzing gene expression data, single-cell sequencing data, and protein-protein interaction networks.
• Image Analysis: It can be applied to reduce the dimensionality of image data, enabling efficient image classification and retrieval.
• Natural Language Processing: UMAP finds applications in natural language processing for reducing the dimensionality of text data, facilitating tasks such as topic modeling and document clustering.

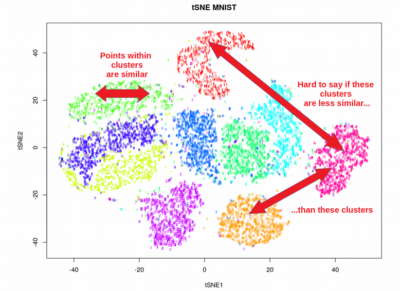
Illustrative Example: Exploring the MNIST Dataset

To illustrate the power of UMAP, let’s consider the MNIST dataset, a classic benchmark in machine learning, containing images of handwritten digits from 0 to 9. Each image consists of 784 pixels, representing a high-dimensional data point.

By applying UMAP to the MNIST dataset, we can reduce the dimensionality to 2, allowing for visualization in a 2D space. The resulting plot reveals distinct clusters corresponding to each digit, showcasing the ability of UMAP to preserve the inherent structure of the data. This visualization not only provides a clear understanding of the data distribution but also highlights the effectiveness of UMAP in capturing non-linear relationships between digits.

Frequently Asked Questions (FAQs) about the UMAP Python Package

Q1: What are the key parameters to adjust in UMAP?

A: The UMAP package offers several adjustable parameters, including:

• n_neighbors: Controls the local neighborhood size used to construct the graph.
• n_components: Determines the dimensionality of the embedding space.
• metric: Specifies the distance metric used to calculate distances between data points.
• min_dist: Influences the density of the embedding space.
• random_state: Allows for reproducible results.

Q2: How can I choose the optimal parameters for my data?

A: The optimal parameters for UMAP depend on the specific dataset and the desired outcome. It is recommended to experiment with different parameter combinations and evaluate the results based on visualization, downstream analysis, or performance metrics.

Q3: How does UMAP compare to other dimensionality reduction techniques like PCA and t-SNE?

A: While PCA focuses on linear relationships, UMAP and t-SNE are non-linear methods. UMAP generally outperforms t-SNE in terms of scalability and preservation of global structure, particularly for large datasets.

Q4: What are some common pitfalls to avoid when using UMAP?

A: Common pitfalls include:

• Overfitting: Choosing a small neighborhood size or a high dimensionality can lead to overfitting, resulting in an embedding that is too specific to the training data.
• Incorrect metric: Using an inappropriate distance metric can distort the embedding and lead to inaccurate results.
• Data preprocessing: Inadequate data preprocessing, such as scaling or normalization, can impact the performance of UMAP.

Tips for Effective UMAP Implementation

• Experiment with different parameter settings: Explore various parameter combinations to find the optimal configuration for your dataset.
• Visualize the results: Use visualization techniques to gain insights into the embedding space and evaluate the effectiveness of UMAP.
• Consider data preprocessing: Apply appropriate preprocessing steps, such as scaling or normalization, to improve the performance of UMAP.
• Use the umap.UMAP class: The umap.UMAP class provides a comprehensive interface for configuring and applying the UMAP algorithm.
• Leverage the umap.plot module: The umap.plot module offers convenient functions for visualizing the embedding space and analyzing the results.

Conclusion

The UMAP Python package provides a powerful and versatile tool for dimensionality reduction, enabling the analysis and visualization of complex, high-dimensional data. Its ability to preserve global structure, handle large datasets efficiently, and provide interpretable results makes it an indispensable tool for researchers and practitioners across various domains. By understanding the core concepts of UMAP and leveraging its features effectively, users can unlock valuable insights from their data and gain a deeper understanding of underlying relationships and patterns. As the field of data analysis continues to evolve, UMAP is poised to play a crucial role in addressing the challenges of dimensionality and unlocking the full potential of data exploration and discovery.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Power of Dimensionality Reduction: A Comprehensive Exploration of the UMAP Python Package. We thank you for taking the time to read this article. See you in our next article!