Unveiling Hidden Structures: A Deep Dive Into UMAP For Dimensionality Reduction

Unveiling Hidden Structures: A Deep Dive into UMAP for Dimensionality Reduction

Related Articles: Unveiling Hidden Structures: A Deep Dive into UMAP for Dimensionality Reduction

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Unveiling Hidden Structures: A Deep Dive into UMAP for Dimensionality Reduction. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling Hidden Structures: A Deep Dive into UMAP for Dimensionality Reduction

The relentless growth of data in the modern world presents a significant challenge for analysis and visualization. High-dimensional datasets, often characterized by numerous features, pose difficulties in understanding underlying patterns and relationships. This is where dimensionality reduction techniques come into play, aiming to simplify complex data by reducing its dimensionality while preserving essential information.

One such powerful technique, gaining widespread popularity in data science, is Uniform Manifold Approximation and Projection (UMAP). This algorithm, implemented in the Python library umap-learn, offers a unique approach to dimensionality reduction, particularly excelling in preserving local neighborhood structures and global relationships within high-dimensional data.

Understanding the Essence of UMAP

At its core, UMAP operates on the principle of finding a low-dimensional representation of data that best preserves the topological structure of the original high-dimensional space. It achieves this by constructing a simplified representation of the data manifold, a geometric object that captures the intrinsic relationships between data points.

The algorithm begins by constructing a graph representation of the data, where each data point is connected to its nearest neighbors. This graph encodes the local neighborhood structure, capturing the proximity and relationships between data points. UMAP then uses a sophisticated mathematical framework, based on Riemannian geometry and fuzzy set theory, to embed this graph into a lower-dimensional space while preserving the local and global relationships.

Key Advantages of UMAP

UMAP stands out for its several advantages over traditional dimensionality reduction techniques like Principal Component Analysis (PCA) and t-Distributed Stochastic Neighbor Embedding (t-SNE):

• Preservation of Local Structure: UMAP excels in preserving local neighborhood structures, ensuring that nearby data points remain close in the reduced space. This is crucial for applications where local relationships are critical, such as clustering and anomaly detection.
• Global Structure Preservation: While preserving local structure, UMAP also maintains global relationships between data points, allowing for the identification of broader patterns and clusters in the reduced space.
• Scalability: UMAP is relatively efficient and scalable, enabling its application to large datasets with millions of data points.
• Interpretability: UMAP’s visualization capabilities allow for a clear and intuitive understanding of the reduced data, facilitating insights into the underlying structure and relationships.
• Flexibility: UMAP can handle diverse data types, including numerical, categorical, and mixed data, making it versatile for various applications.

Applications of UMAP in Data Science

The versatility and effectiveness of UMAP have made it a valuable tool in various data science applications:

• Data Visualization: UMAP excels in visualizing high-dimensional data, enabling researchers to gain insights into the underlying structure, identify clusters, and detect anomalies.
• Clustering: By preserving local and global relationships, UMAP aids in clustering algorithms, enabling the identification of meaningful groups within complex datasets.
• Anomaly Detection: UMAP’s ability to highlight outliers and unusual data points makes it a valuable tool for anomaly detection, particularly in applications where identifying deviations from normal behavior is crucial.
• Feature Engineering: UMAP can be used to create new, lower-dimensional features that capture the essential information from the original high-dimensional dataset, improving the performance of machine learning models.
• Data Exploration: UMAP facilitates data exploration by providing a simplified representation of complex data, allowing researchers to quickly identify patterns and relationships.

Implementation with the umap-learn Library

The umap-learn library provides a user-friendly interface for implementing UMAP in Python. The core function, UMAP(), allows users to customize various parameters, including the number of dimensions for the reduced space, the neighborhood size, and the metric used to measure distances between data points.

Example: Visualizing MNIST Handwritten Digits

Let’s illustrate the power of UMAP by applying it to the MNIST dataset, a benchmark dataset containing handwritten digits.

import umap
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits

# Load the MNIST dataset
digits = load_digits()

# Apply UMAP with 2 dimensions for visualization
reducer = umap.UMAP(n_components=2)
embedding = reducer.fit_transform(digits.data)

# Visualize the embedding
plt.figure(figsize=(8, 6))
plt.scatter(embedding[:, 0], embedding[:, 1], c=digits.target, cmap="viridis")
plt.colorbar()
plt.title("UMAP Embedding of MNIST Digits")
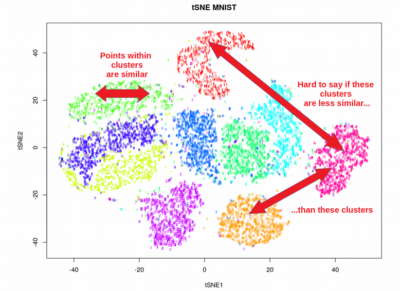
plt.show()

This code snippet applies UMAP to the MNIST dataset, reducing the dimensionality to 2 dimensions for visualization. The resulting scatter plot reveals the separation of handwritten digits based on their visual characteristics.

Understanding the Parameters

The UMAP() function offers numerous parameters for fine-tuning the algorithm. Here are some key parameters:

• n_components: The number of dimensions for the reduced space.
• n_neighbors: The number of nearest neighbors to consider when constructing the graph.
• min_dist: Controls the local crowding of points in the embedding.
• metric: The distance metric used to measure distances between data points.

Frequently Asked Questions (FAQs)

1. When should I use UMAP instead of PCA or t-SNE?

UMAP is a good choice when:

• Local structure is important: UMAP excels at preserving local relationships, making it suitable for applications like clustering and anomaly detection.
• Scalability is a concern: UMAP is more efficient and scalable than t-SNE, particularly for large datasets.

2. How do I choose the optimal number of dimensions for the reduced space?

There is no single answer to this question. It depends on the specific application and the desired level of detail. Experimenting with different values of n_components and evaluating the results based on the specific task is recommended.

3. How do I interpret the UMAP embedding?

The UMAP embedding represents the data in a lower-dimensional space, preserving the local and global relationships between data points. You can interpret the embedding by analyzing the distribution of points, identifying clusters, and looking for outliers.

4. Can I use UMAP for time series data?

Yes, UMAP can be used for time series data, but it may require preprocessing to convert the time series into a suitable format for dimensionality reduction.

5. What are the limitations of UMAP?

• Computational complexity: UMAP can be computationally expensive for very large datasets, especially when using a high number of nearest neighbors.
• Interpretability: While UMAP provides a simplified representation of the data, interpreting the embedding can still be challenging, particularly for complex datasets.

Tips for Using UMAP

• Start with default parameters: The default parameters of UMAP() often provide good initial results.
• Experiment with parameters: Explore different values for n_components, n_neighbors, min_dist, and metric to find the optimal configuration for your specific application.
• Visualize the embedding: Use visualization techniques like scatter plots to gain insights into the reduced data.
• Consider preprocessing: Preprocessing the data, such as scaling or normalization, can improve the performance of UMAP.
• Evaluate the results: Evaluate the performance of UMAP based on the specific task, such as clustering accuracy or anomaly detection performance.

Conclusion

UMAP has emerged as a powerful and versatile dimensionality reduction technique, offering a unique approach to preserving both local and global relationships within high-dimensional data. Its ability to simplify complex data while maintaining essential information makes it a valuable tool for data visualization, clustering, anomaly detection, feature engineering, and data exploration. By leveraging the umap-learn library and understanding its parameters, data scientists can effectively harness the power of UMAP to gain valuable insights from complex datasets and unlock hidden structures within.

Closure

Thus, we hope this article has provided valuable insights into Unveiling Hidden Structures: A Deep Dive into UMAP for Dimensionality Reduction. We appreciate your attention to our article. See you in our next article!