Unraveling the Flat Earth: A Comprehensive Guide to Map Projections
Related Articles: Unraveling the Flat Earth: A Comprehensive Guide to Map Projections
Introduction
In this auspicious occasion, we are delighted to delve into the intriguing topic related to Unraveling the Flat Earth: A Comprehensive Guide to Map Projections. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
Unraveling the Flat Earth: A Comprehensive Guide to Map Projections

The Earth, a sphere suspended in space, presents a unique challenge for cartographers: how to represent its three-dimensional surface on a two-dimensional map. This seemingly simple task is far from straightforward, necessitating the use of map projections.
A map projection is a mathematical transformation that translates the Earth’s curved surface onto a flat plane. This process inevitably introduces distortions, as it is impossible to perfectly represent a sphere on a flat surface without altering some of its properties. Understanding these distortions and their implications is crucial for interpreting maps accurately.
The Underlying Geometry of Map Projections
The heart of map projections lies in geometry. Every projection utilizes a specific mathematical formula to establish a correspondence between points on the Earth’s surface and points on the map plane. These formulas, often complex, are based on a chosen projection surface, which can be a cone, cylinder, or plane.
-
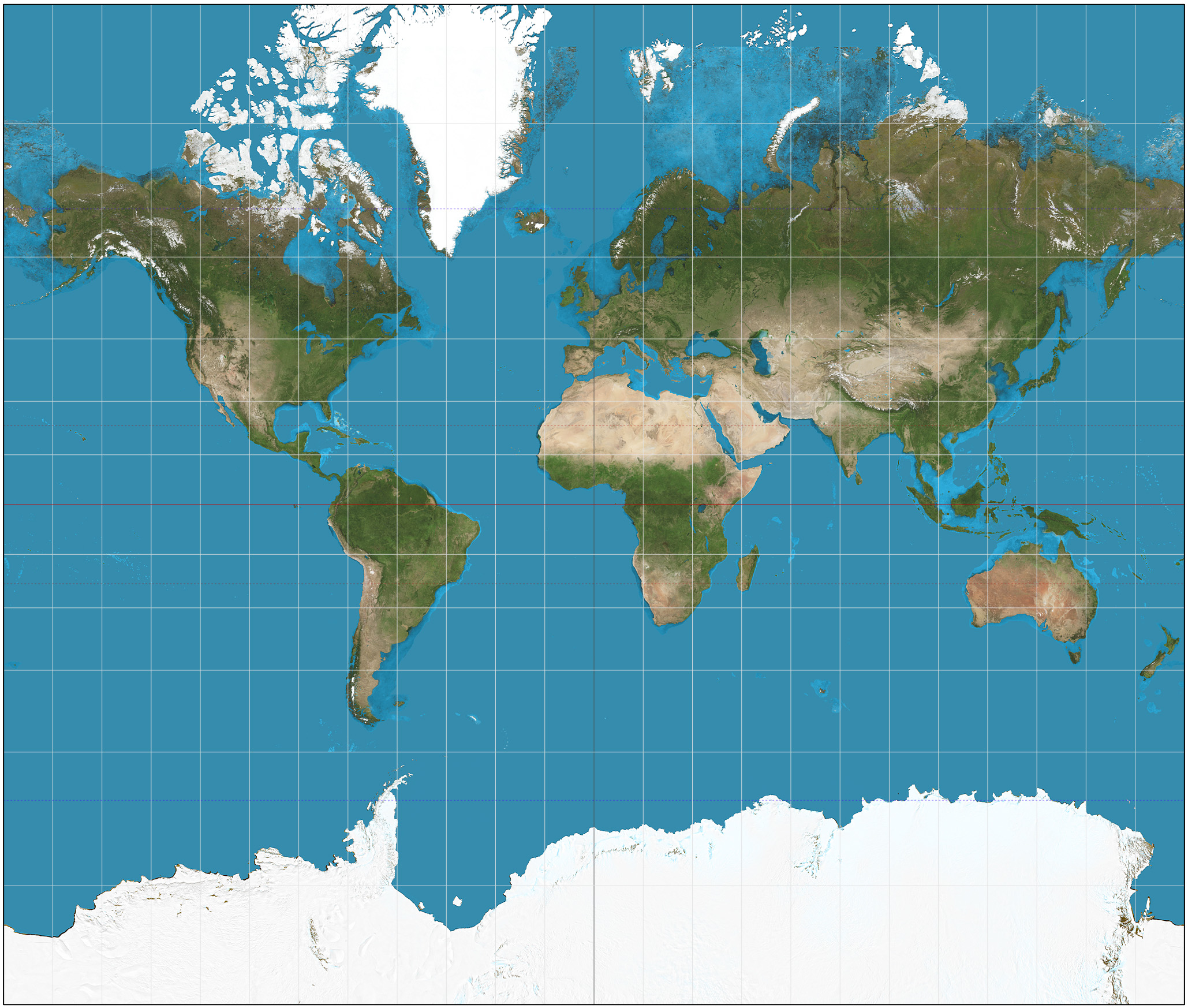
Cylindrical Projections: Imagine wrapping a cylinder around the Earth. Points on the Earth’s surface are projected onto the cylinder, which is then unrolled to create a flat map. This method preserves distances along the equator, but distorts areas and shapes away from the equator. The Mercator projection, commonly used for navigation, is a prime example of a cylindrical projection.
-
Conic Projections: A cone is placed over the Earth, touching it along a chosen line of latitude. Points on the Earth’s surface are projected onto the cone, which is then unrolled. Conic projections preserve shapes and areas along the chosen line of latitude but introduce distortions away from it. They are often used for maps of mid-latitude regions.
-
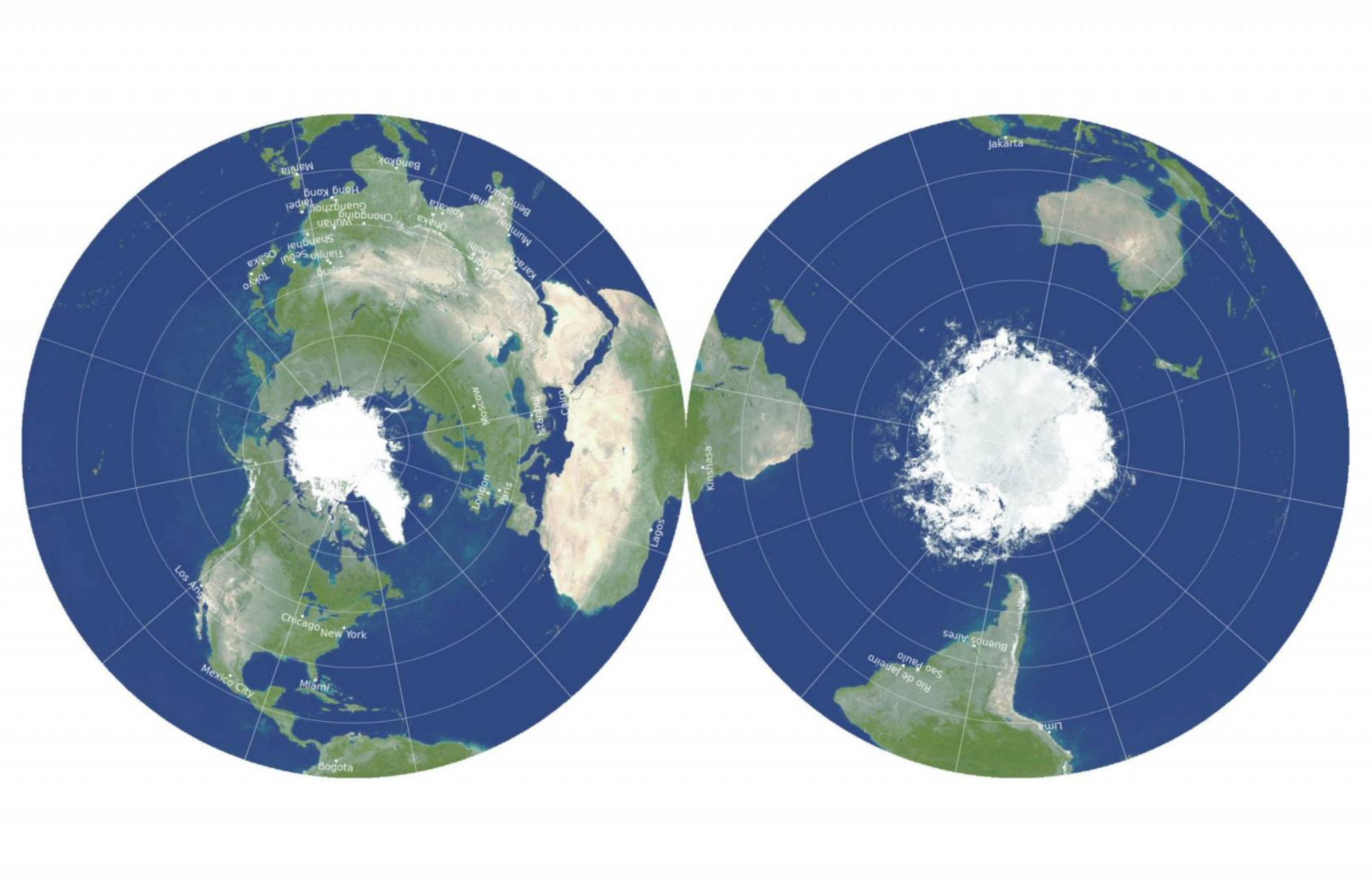
Planar Projections: A plane is tangent to the Earth at a specific point. Points on the Earth’s surface are projected onto the plane, creating a map centered on the chosen point. Planar projections are known as azimuthal projections and are particularly useful for depicting polar regions.
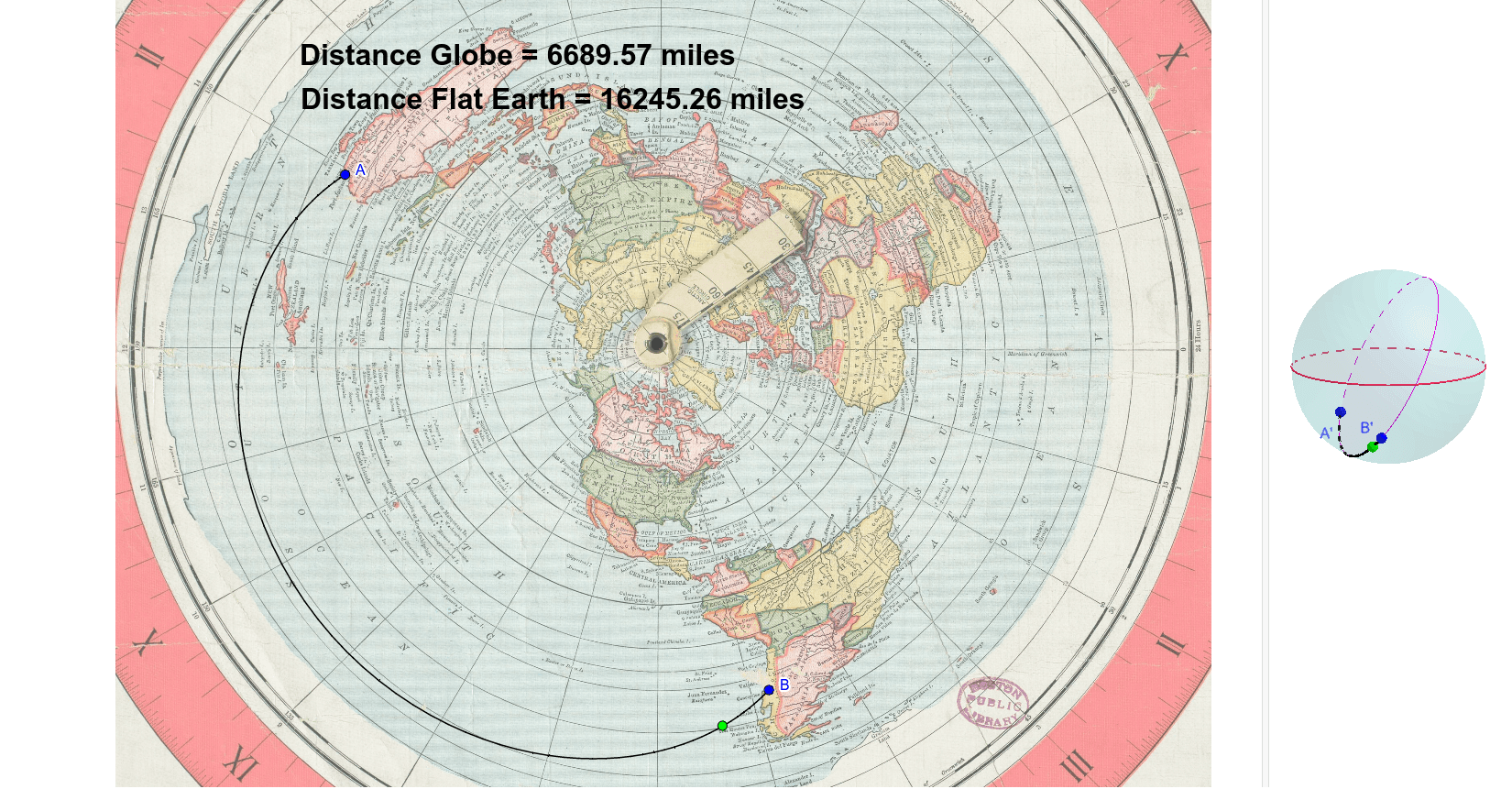
Understanding Distortion: The Trade-offs in Map Projections
As mentioned, no projection can perfectly represent the Earth’s surface without introducing distortions. These distortions affect four key properties:
-
Area: The relative size of landmasses on a map can be distorted. Some projections may exaggerate the size of areas near the poles while shrinking areas near the equator.
-
Shape: The shapes of continents and countries can be distorted. For instance, a projection might stretch Greenland to appear larger than South America, even though it is significantly smaller in reality.
-
Distance: The distances between points on a map can be distorted. Some projections preserve distances along specific lines, while others preserve distances along a network of lines.
-
Direction: The direction of compass bearings can be distorted. This is particularly important for navigation, as a compass reading on a distorted map might not accurately reflect true north.
Choosing the Right Projection: The Art of Balancing Distortion
The choice of projection depends on the specific purpose of the map. There is no single "best" projection; each projection has its strengths and weaknesses. For example:
-
The Mercator Projection: Popular for navigation due to its preservation of angles and compass bearings, it severely distorts areas, making polar regions appear much larger than they actually are.
-
The Gall-Peters Projection: Preserves areas, making it suitable for representing the relative size of continents accurately. However, it distorts shapes and distances.
-
The Robinson Projection: Strives for a balance between area, shape, and distance distortions, making it a good general-purpose projection.
Beyond Traditional Projections: The Rise of Digital Cartography
The advent of digital cartography has opened new possibilities in map projections. Software programs allow for the creation of dynamic projections, where distortions can be minimized or emphasized depending on the specific needs of the user. These programs also enable the creation of interactive maps, allowing users to zoom in, pan, and rotate the map to explore different perspectives.
Frequently Asked Questions (FAQs) on Map Projections
Q: Why do we need map projections?
A: Map projections are essential for representing the Earth’s curved surface on a flat map. They allow us to create maps that are useful for navigation, geographic analysis, and communication.
Q: What are the most common map projections?
A: The Mercator, Gall-Peters, Robinson, and Winkel Tripel projections are among the most commonly used.
Q: How do I choose the right map projection?
A: The best projection depends on the purpose of the map. Consider the type of information you want to convey and the specific distortions that are most important to minimize.
Q: Are there any projections that are completely distortion-free?
A: No, it is impossible to create a map projection that is completely free of distortions. All projections involve compromises.
Q: What are some examples of how map projections are used in everyday life?
A: Map projections are used in a wide range of applications, including:
- Navigation: Maps used for navigation rely on projections that preserve compass bearings and distances.
- Geographic Information Systems (GIS): GIS software uses various projections to analyze and display spatial data.
- Weather Maps: Weather maps use projections that accurately represent the distribution of weather patterns.
- Atlases and Textbooks: Atlases and textbooks use projections that balance area, shape, and distance distortions for general-purpose maps.
Tips for Understanding and Using Map Projections
- Be Aware of Distortion: Always be aware of the distortions inherent in any map projection. Pay attention to the projection used for a particular map and consider its implications.
- Use Multiple Projections: When working with geographic data, it is often helpful to use multiple projections to gain different perspectives.
- Consult with Experts: If you are unsure about the appropriate projection for a specific task, consult with a cartographer or GIS specialist.
Conclusion
Map projections, while often unseen, are fundamental to our understanding of the world. They enable us to visualize the Earth’s surface on a flat plane, allowing for navigation, geographic analysis, and communication. By understanding the principles of map projections and the trade-offs involved in their creation, we can interpret maps more accurately and appreciate the complexity of representing our spherical planet on a two-dimensional surface.





Closure
Thus, we hope this article has provided valuable insights into Unraveling the Flat Earth: A Comprehensive Guide to Map Projections. We hope you find this article informative and beneficial. See you in our next article!