Unlocking The Power Of High-Dimensional Data: A Comprehensive Guide To UMAP In Python

Unlocking the Power of High-Dimensional Data: A Comprehensive Guide to UMAP in Python

Related Articles: Unlocking the Power of High-Dimensional Data: A Comprehensive Guide to UMAP in Python

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Unlocking the Power of High-Dimensional Data: A Comprehensive Guide to UMAP in Python. Let’s weave interesting information and offer fresh perspectives to the readers.

Unlocking the Power of High-Dimensional Data: A Comprehensive Guide to UMAP in Python

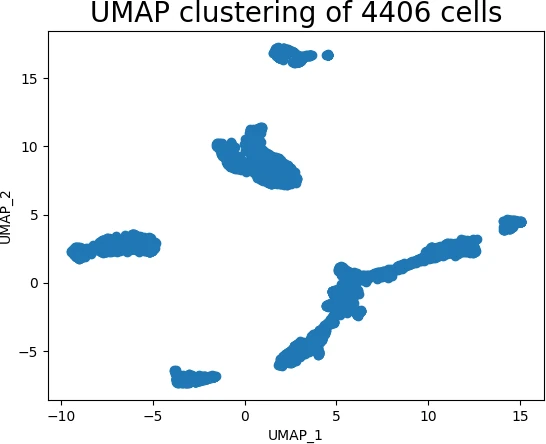
The ability to visualize and understand high-dimensional data is a fundamental challenge in many fields, from machine learning and data science to biology and finance. Traditional methods like Principal Component Analysis (PCA) often struggle to capture the intricate relationships and underlying structure within complex datasets. Enter UMAP, a powerful dimensionality reduction technique that leverages a sophisticated combination of topological data analysis and manifold learning to unveil the hidden patterns within high-dimensional data.

This article delves into the intricacies of UMAP in Python, providing a comprehensive understanding of its principles, implementation, and applications. We will explore its strengths, limitations, and the nuances of its various parameters, equipping readers with the knowledge to confidently harness this powerful tool for their own data analysis endeavors.

Understanding the Essence of UMAP

UMAP, or Uniform Manifold Approximation and Projection, is a non-linear dimensionality reduction technique that excels at preserving the global structure and local relationships within high-dimensional data. It operates on the fundamental premise that high-dimensional data often resides on a low-dimensional manifold embedded within a higher-dimensional space.

Unlike PCA, which focuses on linear relationships and global variance, UMAP aims to uncover the underlying manifold by capturing both the local and global structure of the data. It achieves this through a clever combination of:

• Topological Data Analysis: UMAP employs techniques from topological data analysis to construct a simplicial complex representing the data’s underlying structure. This complex captures the connectivity and relationships between data points, providing a topological representation of the manifold.
• Manifold Learning: UMAP utilizes manifold learning algorithms to project the high-dimensional data onto a lower-dimensional space while preserving the topological structure captured by the simplicial complex. This process ensures that the projected data points retain their original relationships and proximity, even in the reduced dimensionality.

Implementing UMAP in Python: A Practical Walkthrough

Python, with its rich ecosystem of data science libraries, offers a seamless environment for implementing UMAP. The umap library provides a user-friendly interface for applying UMAP to various data analysis tasks.

Installation:

Begin by installing the umap-learn library using pip:

pip install umap-learn

Basic Usage:

The following code snippet illustrates a simple application of UMAP to reduce the dimensionality of a dataset from 10 dimensions to 2:

import umap
import numpy as np

# Generate some sample data
data = np.random.rand(100, 10)

# Initialize UMAP with desired parameters
reducer = umap.UMAP(n_components=2, random_state=42)

# Fit and transform the data
embedding = reducer.fit_transform(data)

# Visualize the reduced data
import matplotlib.pyplot as plt
plt.scatter(embedding[:, 0], embedding[:, 1])
plt.show()

This code demonstrates the core steps involved in using UMAP:

1. Initialization: Create a UMAP object with desired parameters like the target number of dimensions (n_components).
2. Fitting: Train the UMAP model on the input data using the fit_transform method. This step simultaneously fits the model and projects the data onto the lower-dimensional space.
3. Visualization: Visualize the reduced data using a scatter plot, allowing for exploration of the underlying structure revealed by UMAP.

Unraveling the Power of UMAP Parameters: A Deep Dive

The flexibility and effectiveness of UMAP are further enhanced by its customizable parameters. Understanding these parameters allows for fine-tuning the algorithm to optimize its performance for specific datasets and analysis goals.

Key Parameters:

• n_components: This parameter specifies the desired number of dimensions in the reduced representation.
• n_neighbors: This parameter controls the local neighborhood size considered during the manifold learning process. A larger value implies considering a wider neighborhood, potentially leading to smoother and more global representations.
• min_dist: This parameter controls the minimum distance between points in the reduced space. A smaller value leads to more tightly clustered points, while a larger value allows for more spread out representations.
• metric: This parameter defines the distance metric used to calculate the neighborhood structure. Common choices include Euclidean distance, Manhattan distance, and cosine similarity.
• random_state: This parameter allows for setting a seed for random number generation, ensuring reproducibility of results.

Tuning Parameters for Optimal Results:

The optimal values for these parameters depend heavily on the specific dataset and analysis objectives. Experimentation with different parameter combinations is often necessary to achieve the desired results.

• n_neighbors: Experiment with different values to find a balance between capturing local structure and preserving global relationships.
• min_dist: Adjust this parameter to control the degree of crowding in the reduced space.
• metric: Select the metric that best reflects the underlying relationships between data points.

Illuminating the Applications of UMAP: A Diverse Landscape

UMAP’s versatility has led to its widespread adoption in various fields, where it has proven invaluable for understanding and visualizing complex data:

Machine Learning and Data Science:

• Data Visualization: UMAP excels at visualizing high-dimensional data, revealing hidden patterns and clusters that might be obscured in the original space.
• Feature Engineering: UMAP can be used to reduce the dimensionality of data, selecting the most informative features for downstream machine learning tasks.
• Anomaly Detection: UMAP can identify outliers and anomalies by detecting points that lie far from the manifold structure.

Biology and Bioinformatics:

• Single-Cell RNA Sequencing: UMAP enables the visualization and analysis of gene expression data from single cells, uncovering cell types and identifying cellular heterogeneity.
• Protein Structure Analysis: UMAP can be used to visualize protein structures in lower-dimensional spaces, facilitating the analysis of protein folding and interactions.

Finance and Economics:

• Market Analysis: UMAP can be applied to financial data to identify market trends, clusters of companies, and potential investment opportunities.
• Risk Management: UMAP can be used to visualize and analyze risk profiles, identifying potential areas of vulnerability.

Other Applications:

• Image Analysis: UMAP can be used to reduce the dimensionality of image data, enabling efficient image classification and retrieval.
• Text Analysis: UMAP can be applied to text data to visualize semantic relationships between words and documents.

Addressing Common Questions: A Guide to UMAP in Python

Q: How does UMAP handle categorical features?

A: UMAP is primarily designed for continuous data. However, categorical features can be incorporated by encoding them numerically, using techniques like one-hot encoding or ordinal encoding.

Q: What are the computational limitations of UMAP?

A: UMAP’s computational complexity increases with the size and dimensionality of the data. For very large datasets, it might be necessary to use techniques like subsampling or approximate nearest neighbor search to improve efficiency.

Q: How can I evaluate the performance of UMAP?

A: The performance of UMAP can be evaluated using metrics like:

• Visual Inspection: Examining the reduced representation for clusters, patterns, and preservation of relationships.
• Quantitative Measures: Using metrics like silhouette score, Davies-Bouldin index, or K-nearest neighbor accuracy to assess the quality of the embedding.

Q: What are some alternative dimensionality reduction techniques?

A: While UMAP is a powerful tool, other dimensionality reduction techniques like PCA, t-SNE, and Isomap can also be valuable depending on the specific dataset and analysis goals.

Tips for Effective UMAP Implementation:

• Start with a Small Dataset: Begin by applying UMAP to a smaller subset of your data to understand its behavior and tune parameters effectively.
• Experiment with Parameters: Explore different parameter combinations to find the optimal settings for your data.
• Visualize the Results: Always visualize the reduced representation to gain insights into the underlying structure and relationships.
• Consider Alternative Techniques: Explore other dimensionality reduction techniques to find the most suitable approach for your specific needs.

Conclusion: Embracing the Power of UMAP

UMAP stands as a powerful and versatile dimensionality reduction technique that empowers data scientists and researchers to explore and understand complex, high-dimensional datasets. Its ability to preserve both local and global structure while producing visually compelling representations makes it an invaluable tool for a wide range of applications. By leveraging UMAP’s capabilities and understanding its intricacies, researchers can unlock hidden patterns, gain deeper insights, and drive innovation in their respective fields.

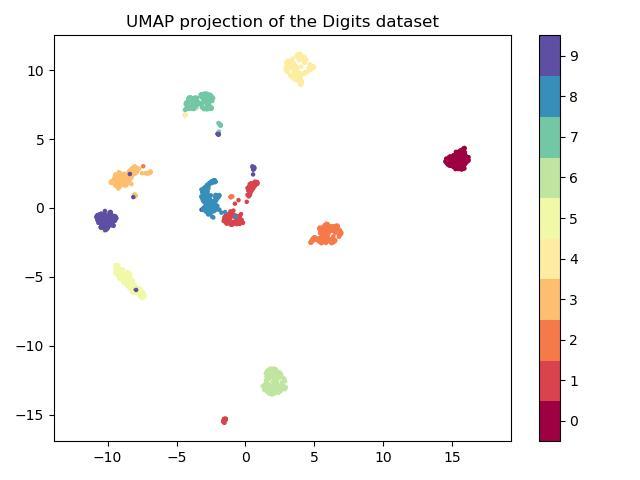
Closure

Thus, we hope this article has provided valuable insights into Unlocking the Power of High-Dimensional Data: A Comprehensive Guide to UMAP in Python. We thank you for taking the time to read this article. See you in our next article!