The Map Coloring Problem: A Python Exploration

The Map Coloring Problem: A Python Exploration

Related Articles: The Map Coloring Problem: A Python Exploration

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to The Map Coloring Problem: A Python Exploration. Let’s weave interesting information and offer fresh perspectives to the readers.

The Map Coloring Problem: A Python Exploration

The map coloring problem is a classic example of a graph coloring problem, a fundamental concept in computer science and mathematics. It involves assigning colors to regions on a map such that no two adjacent regions share the same color. This seemingly simple task holds significant implications for various fields, from resource allocation to network optimization.

This article delves into the map coloring problem, exploring its underlying principles, practical applications, and implementation using Python. We will examine different approaches to solving this problem, including brute force algorithms, backtracking, and greedy algorithms.

Understanding the Problem

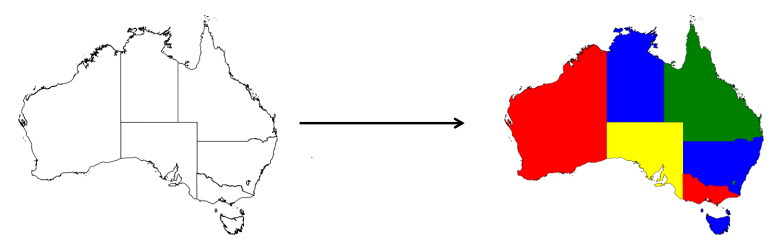
Imagine a map of the United States. Each state represents a distinct region. The goal is to color each state with one of four colors (red, blue, green, and yellow) in such a way that no two adjacent states have the same color. This constraint arises from the need to visually distinguish between neighboring regions.

The map coloring problem can be formally represented as a graph. Each state is a node in the graph, and an edge connects two nodes if the corresponding states share a border. The objective is to assign a color to each node (state) such that no two adjacent nodes (states) have the same color.

The Importance of the Map Coloring Problem

While the map coloring problem might seem like a simple puzzle, its implications extend far beyond geographical maps. Here are some key areas where this problem finds applications:

• Resource Allocation: In resource allocation problems, regions can represent different resources, and colors can represent different types of resources. The map coloring problem helps determine the optimal allocation of resources to ensure no conflicts arise.
• Network Optimization: In network design, nodes can represent computers or servers, and edges can represent connections between them. The map coloring problem can be used to assign different frequencies to communication channels to avoid interference.
• Scheduling: In scheduling tasks, regions can represent different tasks, and colors can represent different time slots. The map coloring problem helps schedule tasks in a way that avoids conflicts.
• Computer Graphics: The map coloring problem is also used in computer graphics to efficiently render images by assigning different colors to adjacent pixels.

Solving the Map Coloring Problem with Python

Python provides a powerful platform for solving the map coloring problem. Here’s a breakdown of the different approaches:

1. Brute Force Algorithm

The brute force approach is the most straightforward but computationally expensive method. It involves systematically trying all possible color combinations for each region until a valid solution is found. This approach quickly becomes impractical as the number of regions increases.

def is_valid_coloring(coloring, graph):
    """
    Checks if a given coloring is valid for the given graph.
    """
    for node in graph:
        for neighbor in graph[node]:
            if coloring[node] == coloring[neighbor]:
                return False
    return True

def brute_force_coloring(graph, colors):
    """
    Solves the map coloring problem using a brute force approach.
    """
    num_nodes = len(graph)
    for coloring in itertools.product(colors, repeat=num_nodes):
        if is_valid_coloring(coloring, graph):
            return coloring
    return None

# Example graph representation
graph = 
    'A': ['B', 'C'],
    'B': ['A', 'C', 'D'],
    'C': ['A', 'B', 'D', 'E'],
    'D': ['B', 'C', 'E'],
    'E': ['C', 'D']


# Available colors
colors = ['Red', 'Blue', 'Green', 'Yellow']

# Solve using brute force
coloring = brute_force_coloring(graph, colors)
print(coloring)

2. Backtracking Algorithm

Backtracking is a more efficient approach than brute force. It involves building a solution incrementally, checking for validity at each step. If a step leads to a conflict, the algorithm backtracks to the previous step and tries a different option.

def is_valid_color(node, color, coloring, graph):
    """
    Checks if a given color is valid for a given node.
    """
    for neighbor in graph[node]:
        if coloring[neighbor] == color:
            return False
    return True

def backtrack_coloring(node, coloring, graph, colors):
    """
    Solves the map coloring problem using backtracking.
    """
    if node == len(graph):
        return coloring

    for color in colors:
        if is_valid_color(node, color, coloring, graph):
            coloring[node] = color
            result = backtrack_coloring(node + 1, coloring, graph, colors)
            if result is not None:
                return result
            coloring[node] = None  # Backtrack

    return None

# Example graph representation
graph = 
    'A': ['B', 'C'],
    'B': ['A', 'C', 'D'],
    'C': ['A', 'B', 'D', 'E'],
    'D': ['B', 'C', 'E'],
    'E': ['C', 'D']


# Available colors
colors = ['Red', 'Blue', 'Green', 'Yellow']

# Solve using backtracking
coloring = backtrack_coloring(0, [None] * len(graph), graph, colors)
print(coloring)

3. Greedy Algorithm

Greedy algorithms aim to find a solution by making locally optimal choices at each step. In the map coloring problem, a greedy algorithm assigns colors to regions one by one, choosing the color that minimizes conflicts with already colored neighbors.

def greedy_coloring(graph, colors):
    """
    Solves the map coloring problem using a greedy algorithm.
    """
    coloring = 
    for node in graph:
        available_colors = colors.copy()
        for neighbor in graph[node]:
            if neighbor in coloring:
                available_colors.remove(coloring[neighbor])
        coloring[node] = available_colors[0]
    return coloring

# Example graph representation
graph = 
    'A': ['B', 'C'],
    'B': ['A', 'C', 'D'],
    'C': ['A', 'B', 'D', 'E'],
    'D': ['B', 'C', 'E'],
    'E': ['C', 'D']


# Available colors
colors = ['Red', 'Blue', 'Green', 'Yellow']

# Solve using greedy algorithm
coloring = greedy_coloring(graph, colors)
print(coloring)

Evaluating the Approaches

Each approach has its strengths and weaknesses:

• Brute Force: Simple to implement, but computationally expensive, especially for large graphs.
• Backtracking: More efficient than brute force, but can still be slow for complex graphs.
• Greedy: Fast and relatively easy to implement, but might not always find the optimal solution.

The choice of approach depends on the size and complexity of the map, the desired level of accuracy, and the available computational resources.

Beyond Basic Implementation: Advanced Considerations

While the provided code demonstrates basic implementations of different approaches, solving real-world map coloring problems often requires additional considerations:

• Graph Data Structures: Efficient representation of the graph is crucial for performance. Data structures like adjacency lists or adjacency matrices are commonly used.
• Color Ordering: The order in which colors are considered can significantly affect the performance of greedy algorithms. Heuristics like assigning the least frequently used color first can improve efficiency.
• Optimization Techniques: For large graphs, techniques like constraint satisfaction problems (CSP) and graph partitioning can be used to improve the efficiency of the solution process.

FAQs about the Map Coloring Problem and Python Code

1. What is the Four Color Theorem?

The Four Color Theorem states that any map can be colored with at most four colors such that no two adjacent regions share the same color. This theorem has been rigorously proven, but the proof is complex and involves advanced mathematical techniques.

2. Can the Map Coloring Problem always be solved?

Yes, the map coloring problem can always be solved for any valid map. However, the number of colors required may vary depending on the complexity of the map.

3. How can I represent a map as a graph in Python?

You can represent a map as a graph using dictionaries. Each key in the dictionary represents a region, and the corresponding value is a list of its neighboring regions.

4. What are some libraries that can help solve the Map Coloring Problem in Python?

Libraries like networkx and graph_tool provide tools for graph manipulation and analysis, which can be helpful for solving the map coloring problem.

5. What are some real-world applications of the Map Coloring Problem?

Besides the examples mentioned earlier, the map coloring problem finds applications in areas like resource allocation, scheduling, frequency assignment, and data visualization.

Tips for Solving the Map Coloring Problem in Python

• Start with a simple example: Implement the code for a small map with a few regions to understand the core concepts.
• Choose the right data structure: Select a data structure that efficiently represents the map as a graph.
• Optimize the algorithm: Explore different approaches and optimization techniques to improve the efficiency of your solution.
• Test your code thoroughly: Use a variety of test cases to ensure your code produces accurate and efficient results.

Conclusion

The map coloring problem is a fascinating problem that highlights the power of graph theory and computational algorithms. While seemingly simple, its applications extend to various domains, making it a valuable tool for optimizing resources, scheduling tasks, and solving real-world problems. Python, with its rich libraries and expressive syntax, provides an ideal platform for exploring and solving this problem, offering a glimpse into the world of graph coloring and its practical implications.

Closure

Thus, we hope this article has provided valuable insights into The Map Coloring Problem: A Python Exploration. We thank you for taking the time to read this article. See you in our next article!