The Art of Preserving Shape: A Deep Dive into Conformal Map Projections
Related Articles: The Art of Preserving Shape: A Deep Dive into Conformal Map Projections
Introduction
In this auspicious occasion, we are delighted to delve into the intriguing topic related to The Art of Preserving Shape: A Deep Dive into Conformal Map Projections. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
The Art of Preserving Shape: A Deep Dive into Conformal Map Projections
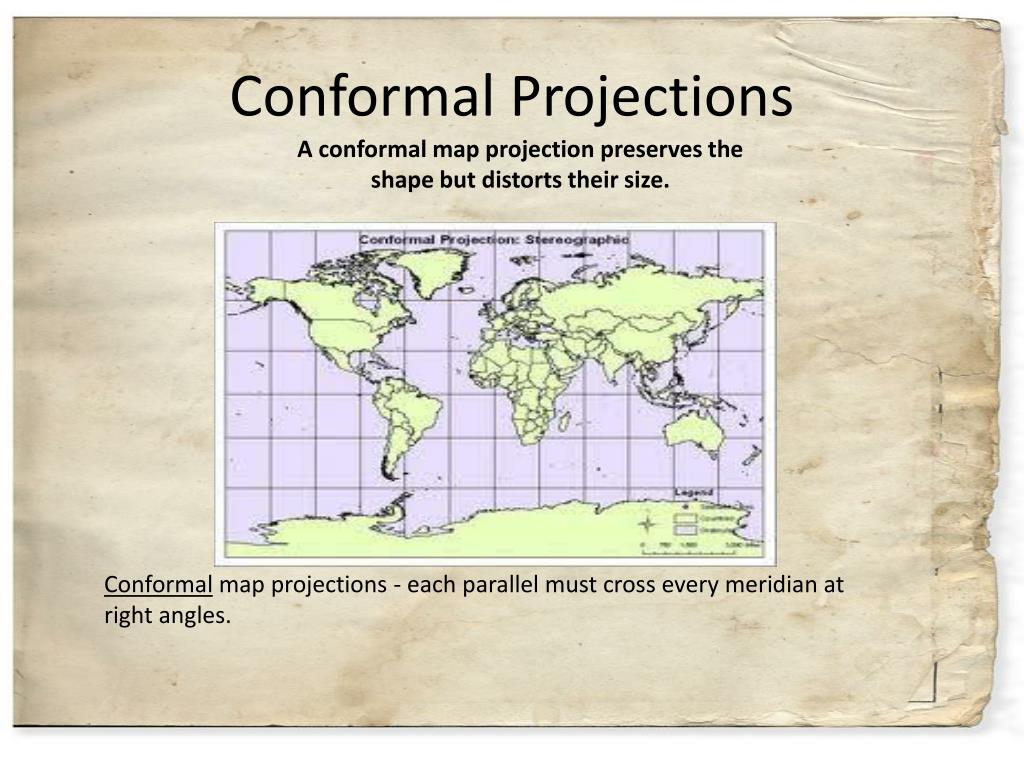
The Earth, a sphere of unparalleled beauty and complexity, presents a unique challenge for cartographers. To depict its vastness on a flat surface, we rely on map projections, mathematical transformations that translate the Earth’s curved surface onto a plane. While these projections offer a practical representation of our planet, they inevitably introduce distortions. Some projections prioritize area, others distance, and some aim to preserve the shapes of features. This article delves into the fascinating world of conformal map projections, exploring their strengths, limitations, and applications.
Conformal Projections: Preserving Angles and Shapes
Conformal projections are renowned for their ability to maintain the correct angles between lines at any point on the map. This angle preservation, known as conformality, translates into accurate representation of shapes, especially for small areas. The key to achieving this lies in the projection’s mathematical properties. Conformal projections ensure that the scale at any point on the map is the same in all directions. This means that a circle on the Earth’s surface will be projected as a circle on the map, albeit with a potentially different size.
A Closer Look at the Mathematics
The mathematical basis of conformal projections lies in the use of complex numbers. These numbers, consisting of a real and an imaginary component, allow for elegant representation of geometric transformations. Conformal projections rely on the concept of "conformal mapping," where the complex derivative of the transformation function is a non-zero real number. This ensures that angles are preserved during the projection.
Exploring Popular Conformal Projections
Several conformal projections have gained widespread use due to their unique strengths and applications. Some notable examples include:
-
Mercator Projection: The Mercator projection, perhaps the most famous conformal projection, is known for its rectangular grid and preservation of compass directions. However, its major drawback lies in the significant distortion of areas, especially towards the poles. This makes it unsuitable for representing global phenomena like climate patterns or population density.
-
Stereographic Projection: The stereographic projection, a conformal projection that maps the Earth onto a plane tangent to a point on the sphere, offers an accurate representation of shapes, especially near the point of tangency. It is often used in cartographic applications requiring precise shape preservation, such as nautical charts.
-
Lambert Conformal Conic Projection: This projection, often used for mapping large areas with minimal distortion, utilizes a cone to represent the Earth. It is particularly useful for mapping countries spanning large latitudinal ranges, such as the United States.
-
Transverse Mercator Projection: This projection, a variant of the Mercator projection, uses a cylinder tangent to the Earth along a meridian. It is widely used for mapping narrow areas, such as countries with elongated shapes, as it minimizes distortion along the central meridian.
Benefits of Conformal Projections
The ability of conformal projections to preserve shapes offers several advantages:
-
Accurate Representation of Features: Conformal projections excel in representing small-scale features, such as coastlines, rivers, and cities, with minimal distortion. This accuracy is crucial for applications requiring precise detail, like navigation, land surveying, and urban planning.
-
Preservation of Angles: The preservation of angles is particularly beneficial for applications involving directions and bearings. Navigation charts, for instance, rely on conformal projections to ensure accurate representation of compass headings and course lines.
-
Ease of Interpretation: Conformal projections, with their accurate representation of shapes, make maps easier to interpret and understand. Features on the map appear more natural and familiar, facilitating spatial analysis and decision-making.
Limitations of Conformal Projections
While conformal projections excel in preserving shapes, they are not without limitations:
-
Area Distortion: The preservation of angles comes at the cost of area distortion. Conformal projections tend to exaggerate areas further from the point of tangency or the central meridian, leading to misrepresentations of relative sizes.
-
Limited Global Representation: Conformal projections are often designed for specific regions or areas, making them less suitable for representing the entire globe. The distortion in areas far from the point of tangency or the central meridian can become significant, rendering the projection less accurate for global applications.
-
Complexity of Construction: Conformal projections often involve complex mathematical calculations, requiring specialized software and expertise for their construction and use.
FAQs about Conformal Projections
1. What is the difference between a conformal projection and an equal-area projection?
Conformal projections prioritize the preservation of angles and shapes, while equal-area projections aim to maintain the relative sizes of areas on the map. Conformal projections typically distort areas, while equal-area projections distort shapes.
2. Why is the Mercator projection still widely used despite its area distortion?
The Mercator projection’s rectangular grid and preservation of compass directions make it convenient for navigation and map making. Its widespread use in online mapping services and atlases has contributed to its continued popularity, despite its limitations.
3. Are there any projections that combine the benefits of conformal and equal-area projections?
While no projection can perfectly achieve both conformality and equal-area preservation, some projections attempt to balance these properties. The Winkel Tripel projection, for example, aims to minimize both area and shape distortion, although it does not achieve perfect preservation of either.
4. How are conformal projections used in real-world applications?
Conformal projections are essential in various fields:
- Navigation: Nautical charts and aviation maps rely on conformal projections to ensure accurate representation of compass bearings and course lines.
- Land Surveying: Conformal projections are used for accurate land measurements and mapping, crucial for property boundaries and infrastructure development.
- Urban Planning: Conformal projections provide detailed representations of urban environments, facilitating infrastructure planning and urban design.
- Climate Modeling: Conformal projections are used in climate modeling to represent weather patterns and atmospheric processes with minimal shape distortion.
Tips for Choosing the Right Conformal Projection
Selecting the appropriate conformal projection depends on the specific application and the area being mapped:
- Consider the Area of Interest: Choose a projection that minimizes distortion within the region being mapped.
- Evaluate the Purpose of the Map: Select a projection that prioritizes the required properties, whether it’s shape preservation, area accuracy, or compass directions.
- Consult with a Cartographer: For complex applications, seeking expert advice from a cartographer can help choose the most suitable projection.
Conclusion
Conformal map projections play a crucial role in representing the Earth’s surface accurately, especially when preserving shapes is paramount. From navigation charts to urban planning maps, these projections offer valuable tools for visualizing and analyzing spatial data. Understanding their strengths, limitations, and applications is essential for selecting the most appropriate projection for a given task, ensuring accurate and meaningful representations of our planet. The art of map projections continues to evolve, with ongoing research exploring new techniques and approaches to achieve even more accurate and insightful representations of the Earth’s intricate tapestry.







Closure
Thus, we hope this article has provided valuable insights into The Art of Preserving Shape: A Deep Dive into Conformal Map Projections. We thank you for taking the time to read this article. See you in our next article!