Projection Map Topology: A Comprehensive Guide
Related Articles: Projection Map Topology: A Comprehensive Guide
Introduction
With great pleasure, we will explore the intriguing topic related to Projection Map Topology: A Comprehensive Guide. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
Projection Map Topology: A Comprehensive Guide
![]()
Projection map topology, a fundamental concept in topology, provides a powerful framework for understanding and analyzing complex spaces. It enables us to study the relationship between spaces and their "shadows" – projections – offering invaluable insights into their geometric and topological properties. This article delves into the intricacies of projection map topology, elucidating its core concepts, applications, and implications.
Understanding Projection Maps
The foundation of projection map topology lies in the concept of a projection map. A projection map is a function that "projects" points from one space onto another, essentially creating a "shadow" of the original space. This projection can be visualized as a mapping from a higher-dimensional space to a lower-dimensional space, where certain dimensions are "lost" in the process.
Types of Projection Maps:
Projection maps come in various forms, each with its unique properties and applications. Here are some common types:
- Orthogonal Projections: These project points onto a subspace perpendicular to the original space. This is similar to casting a shadow with a light source directly above the object.
- Perspective Projections: These project points from a point of view, creating a more realistic representation of three-dimensional objects on a two-dimensional surface. This is analogous to the way we perceive the world through our eyes.
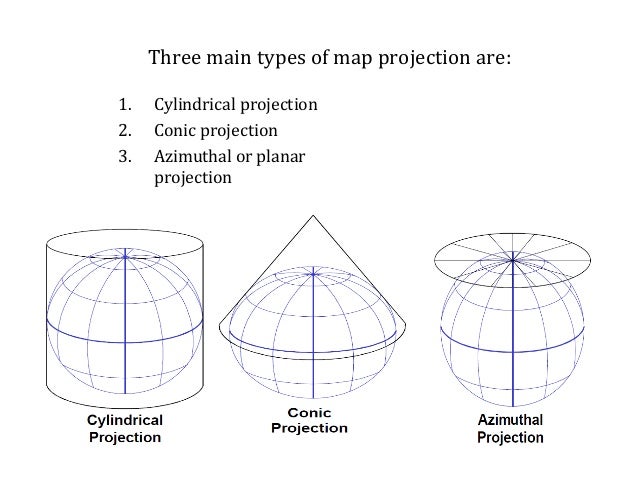
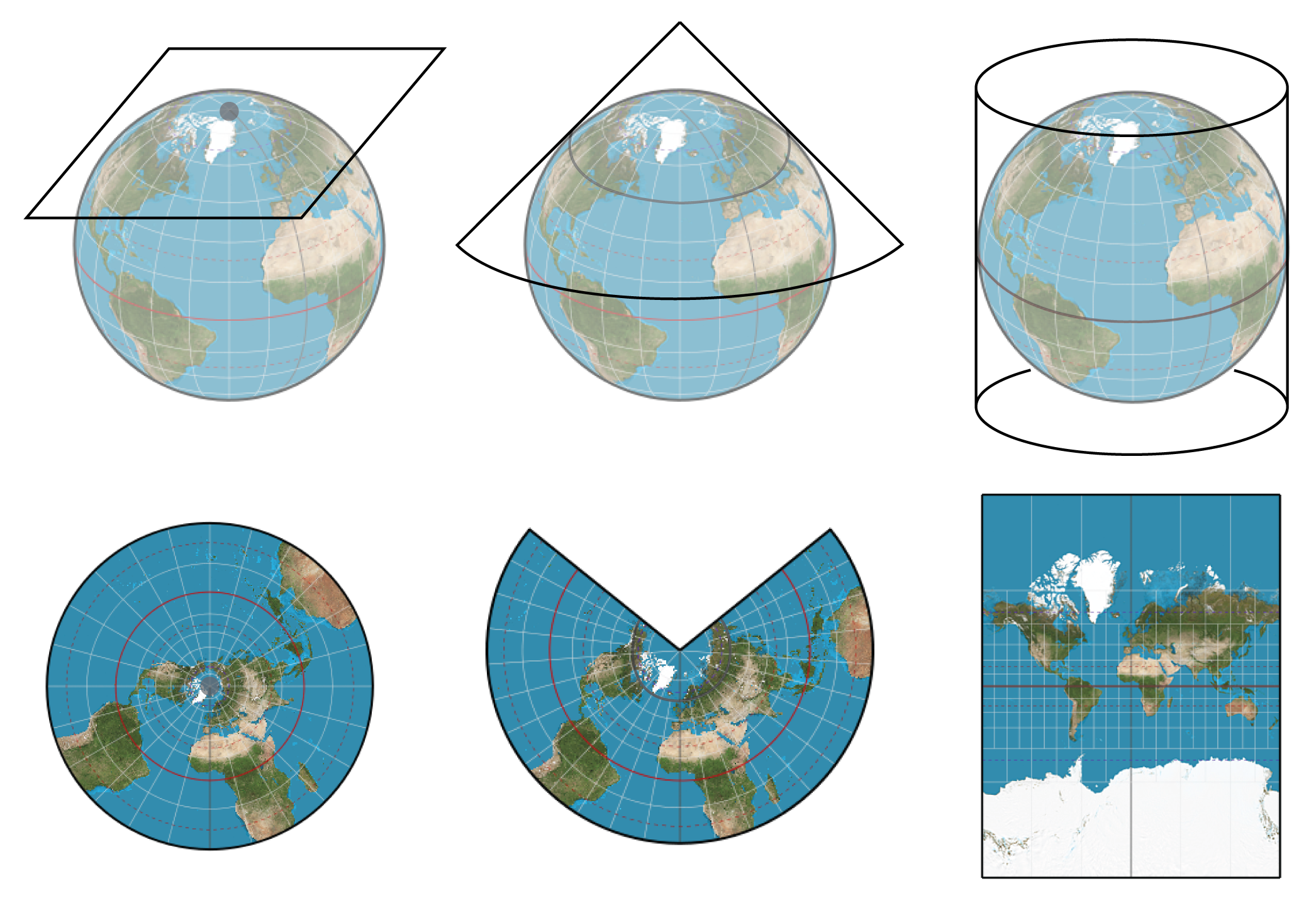
- Stereographic Projections: These project points from a sphere onto a plane, preserving angles but distorting distances. This technique is widely used in cartography to represent the Earth’s surface on a flat map.
Projection Map Topology: Connecting Spaces and Their Shadows
Projection map topology explores the relationships between spaces and their projections. It analyzes how topological properties of the original space are preserved or distorted in the projected space. This analysis reveals crucial information about the structure of the original space and its relationship to the projected space.
Key Concepts in Projection Map Topology:
- Continuity: A projection map is continuous if small changes in the original space result in small changes in the projected space. This property ensures that the projected space preserves the essential features of the original space.
- Openness and Closedness: Projection maps can preserve or distort open and closed sets in the original space. Understanding how these properties are affected by the projection helps us analyze the topology of the projected space.
- Homeomorphism: A projection map is a homeomorphism if it is continuous, bijective (one-to-one and onto), and its inverse is also continuous. In this case, the projected space is topologically equivalent to the original space, meaning they have the same topological properties.
Applications of Projection Map Topology:
Projection map topology finds applications in various fields, including:
- Geometry: Projection maps are essential tools for studying geometric shapes and their properties. By projecting higher-dimensional objects onto lower-dimensional spaces, we can gain insights into their structure and relationships.
- Topology: Projection map topology helps us understand the topological properties of spaces and how they are preserved or distorted under various projections. This knowledge is crucial for classifying and analyzing topological spaces.
- Data Analysis: Projection maps are used in data visualization and dimensionality reduction techniques. By projecting high-dimensional data onto lower-dimensional spaces, we can identify patterns, clusters, and trends that might be obscured in the original data.
- Computer Graphics: Projection maps play a critical role in computer graphics, enabling the rendering of three-dimensional objects on two-dimensional screens. Perspective projections, in particular, create realistic representations of objects by simulating the way our eyes perceive the world.
Benefits of Projection Map Topology:
The application of projection map topology offers numerous benefits:
- Simplification: Projection maps allow us to simplify complex spaces by projecting them onto lower-dimensional spaces, making them easier to analyze and understand.
- Visualization: Projection maps facilitate the visualization of high-dimensional data and spaces, making it possible to identify patterns and relationships that might be hidden in the original data.
- Dimensionality Reduction: Projection maps are used to reduce the dimensionality of data, making it easier to process and analyze. This is particularly useful in machine learning and data mining.
- Geometric Insights: Projection maps provide valuable insights into the geometric properties of spaces, revealing their structure, symmetries, and relationships.
FAQs on Projection Map Topology
1. What is the difference between a projection map and a homomorphism?
A projection map is a function that maps points from one space to another, often preserving certain properties. A homomorphism, on the other hand, is a function that preserves the algebraic structure of the spaces involved. While both types of maps can be used to study relationships between spaces, they focus on different aspects.
2. How can I determine if a projection map preserves a particular topological property?
To determine whether a projection map preserves a topological property, you need to analyze how the map affects the property in question. For example, if you want to know if the projection preserves open sets, you need to examine whether the image of an open set in the original space is also open in the projected space.
3. What are some examples of spaces that can be studied using projection map topology?
Projection map topology can be applied to study a wide variety of spaces, including Euclidean spaces, manifolds, topological groups, and even more abstract spaces. The specific applications depend on the type of projection map used and the properties of the spaces being studied.
4. How does projection map topology relate to other areas of mathematics?
Projection map topology is closely related to other areas of mathematics, such as geometry, topology, and algebra. It provides a framework for studying relationships between spaces and their projections, which can be used to gain insights into various mathematical concepts.
Tips for Studying Projection Map Topology
- Start with basic examples: Begin by studying simple examples of projection maps, such as orthogonal projections and perspective projections, to gain a foundational understanding of the concepts.
- Focus on properties: Pay close attention to how projection maps affect various topological properties, such as continuity, openness, closedness, and homeomorphism.
- Visualize the concepts: Use diagrams and visualizations to help understand how projection maps work and how they relate to the spaces being studied.
- Connect to real-world applications: Explore how projection map topology is used in different fields, such as geometry, computer graphics, and data analysis, to gain a deeper appreciation for its practical applications.
Conclusion
Projection map topology offers a powerful framework for analyzing and understanding the relationships between spaces and their projections. By studying how topological properties are preserved or distorted under different projection maps, we gain valuable insights into the structure and relationships of spaces. This field has applications in various areas of mathematics, computer science, and other disciplines, making it a vital tool for exploring and understanding the intricate world of topology.

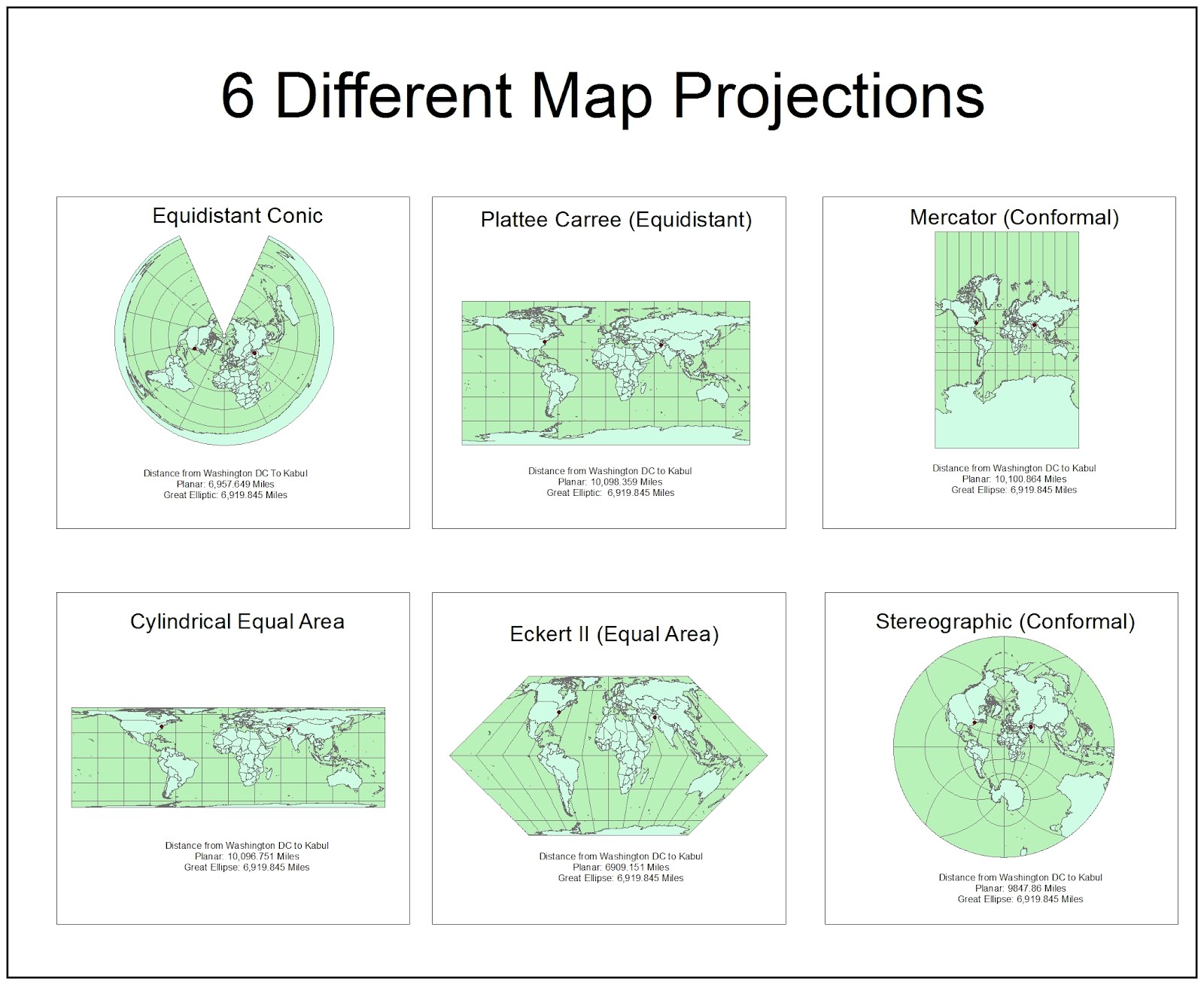
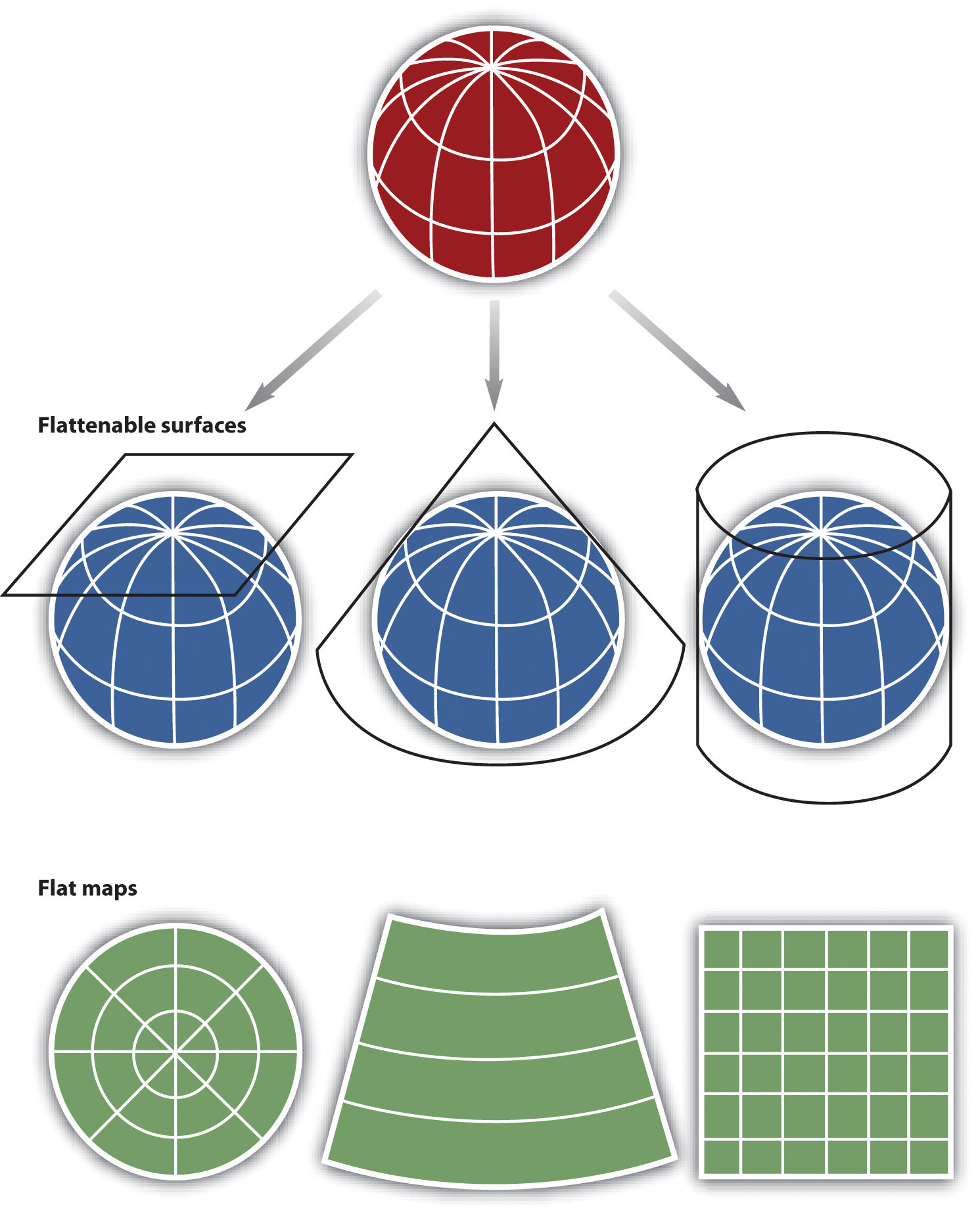

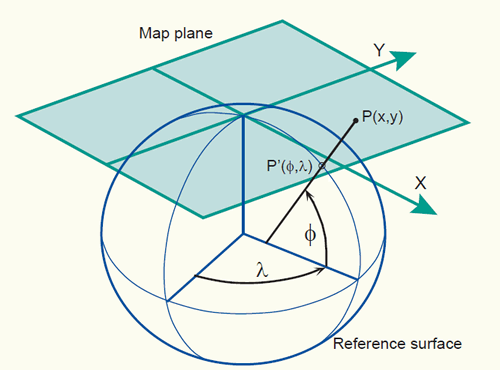
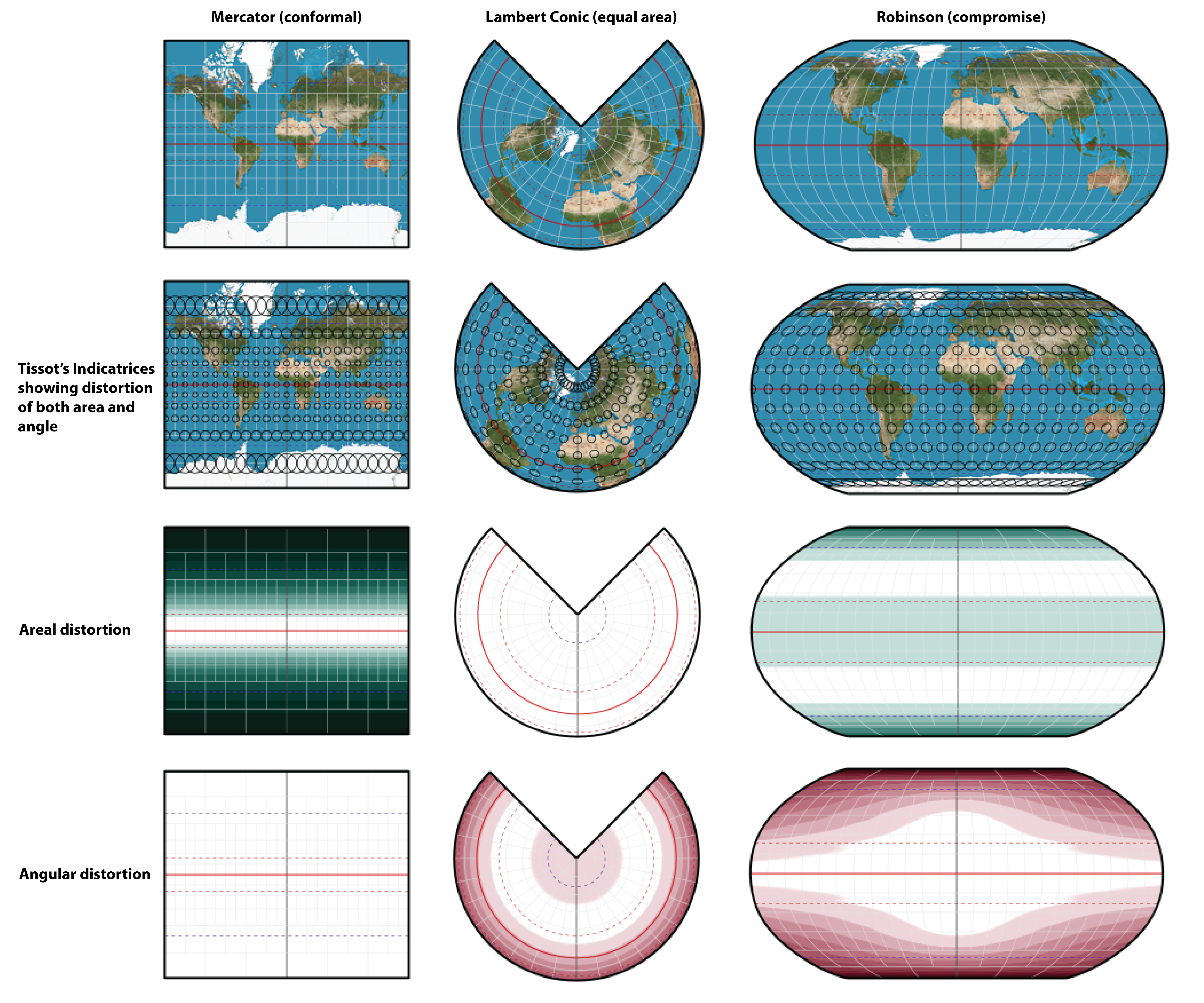
Closure
Thus, we hope this article has provided valuable insights into Projection Map Topology: A Comprehensive Guide. We appreciate your attention to our article. See you in our next article!