Navigating The Landscape Of Dimensionality Reduction: A Guide To Installing And Utilizing UMAP In Python

Navigating the Landscape of Dimensionality Reduction: A Guide to Installing and Utilizing UMAP in Python

Related Articles: Navigating the Landscape of Dimensionality Reduction: A Guide to Installing and Utilizing UMAP in Python

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Navigating the Landscape of Dimensionality Reduction: A Guide to Installing and Utilizing UMAP in Python. Let’s weave interesting information and offer fresh perspectives to the readers.

Navigating the Landscape of Dimensionality Reduction: A Guide to Installing and Utilizing UMAP in Python

The realm of data science is often characterized by the overwhelming abundance of information. Datasets, particularly in the modern era, frequently possess a high number of dimensions, posing significant challenges to analysis and visualization. This is where dimensionality reduction techniques come into play, offering a powerful means to simplify complex datasets while preserving their inherent structure. Among these techniques, Uniform Manifold Approximation and Projection (UMAP) has emerged as a robust and versatile tool, gaining widespread recognition for its ability to efficiently uncover hidden patterns and create insightful visualizations.

This comprehensive guide delves into the intricacies of installing and utilizing UMAP in the Python programming language, equipping readers with the knowledge and skills to effectively harness its capabilities. We will explore the foundational principles of UMAP, its advantages over traditional methods, and practical steps for successful implementation.

Understanding UMAP: A Glimpse into its Power

UMAP is a non-linear dimensionality reduction technique that excels at preserving the global structure of data while maintaining local neighborhood relationships. Its underlying principle rests on the assumption that high-dimensional data often resides on a low-dimensional manifold, a smooth, continuous surface embedded within the higher dimensional space. UMAP seeks to unravel this underlying structure, projecting the data onto a lower-dimensional space while retaining the essential topological features.

Benefits of UMAP: Unveiling the Advantages

UMAP offers a compelling set of advantages that distinguish it from other dimensionality reduction techniques:

• Preservation of Global Structure: UMAP effectively captures the global relationships within the data, ensuring that distant points in the original high-dimensional space remain relatively far apart in the lower-dimensional representation. This is crucial for maintaining the overall context and understanding of the data.

• Emphasis on Local Neighborhoods: UMAP prioritizes the preservation of local neighborhood relationships, ensuring that points close to each other in the high-dimensional space remain close in the lower-dimensional representation. This property is particularly valuable for visualizing and analyzing data with complex local structures.

• Speed and Efficiency: UMAP is remarkably efficient, capable of handling large datasets with speed and accuracy. This efficiency stems from its optimized algorithms and the clever use of graph-based representations.

• Intuitive Parameterization: UMAP offers a limited number of parameters, making it relatively easy to tune and optimize for specific datasets. This ease of use further enhances its practicality and accessibility.

Installation and Implementation: A Step-by-Step Guide

Installing UMAP in Python is a straightforward process, typically requiring just a few commands. The most common approach involves utilizing the pip package manager:

pip install umap-learn

This command will download and install the UMAP library along with its dependencies. Once installed, you can import and utilize the UMAP algorithm within your Python scripts.

A Practical Example: Unveiling the Power of UMAP in Action

Let’s consider a hypothetical scenario where we have a dataset containing information about various types of flowers. Each flower is represented by a set of features, such as petal length, petal width, sepal length, and sepal width. This dataset, while informative, is challenging to visualize directly due to its four-dimensional nature.

import pandas as pd
import umap

# Load the flower dataset
data = pd.read_csv("flowers.csv")

# Extract the features for dimensionality reduction
features = data[["petal_length", "petal_width", "sepal_length", "sepal_width"]]

# Create a UMAP object
reducer = umap.UMAP()

# Fit the UMAP model to the data
embedding = reducer.fit_transform(features)

# Visualize the reduced data
import matplotlib.pyplot as plt
plt.scatter(embedding[:, 0], embedding[:, 1], c=data["species"])
plt.xlabel("UMAP Dimension 1")
plt.ylabel("UMAP Dimension 2")
plt.title("UMAP Visualization of Flower Dataset")
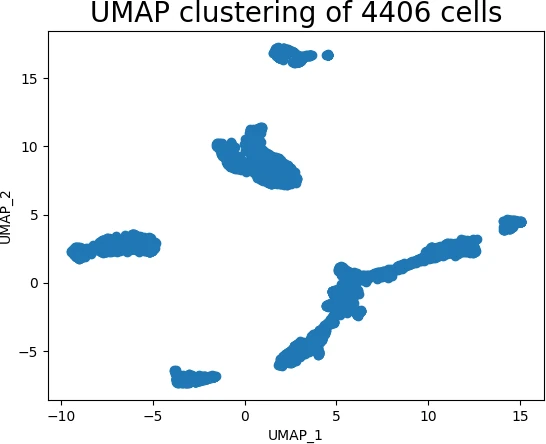
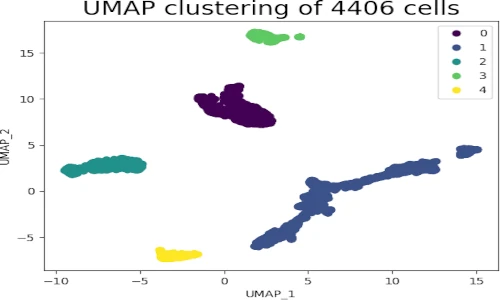
plt.show()

This code snippet demonstrates the ease of using UMAP. We first import the necessary libraries, including pandas for data handling and umap for dimensionality reduction. After loading the dataset, we extract the relevant features and create a UMAP object. The fit_transform method then applies the UMAP algorithm to the data, generating a lower-dimensional representation. Finally, we visualize the reduced data using a scatter plot, revealing the hidden patterns and relationships within the dataset.

Navigating the Landscape of UMAP Parameters

UMAP offers a set of adjustable parameters that allow for fine-tuning its behavior to suit specific datasets and analysis goals. Understanding these parameters is crucial for achieving optimal results:

• n_neighbors: This parameter controls the size of the local neighborhood considered during the dimensionality reduction process. A higher value leads to a larger neighborhood, capturing more global structure.

• min_dist: This parameter determines the minimum distance between points in the lower-dimensional space. A higher value results in greater separation between points, emphasizing local structures.

• metric: This parameter specifies the distance metric used to calculate distances between points in the original high-dimensional space. Common options include Euclidean distance, Manhattan distance, and cosine similarity.

• n_components: This parameter defines the number of dimensions in the lower-dimensional representation. By default, UMAP reduces the data to two dimensions for ease of visualization.

Addressing Common Questions: A Comprehensive FAQ

Q: What are the limitations of UMAP?

A: While UMAP is a powerful tool, it’s important to acknowledge its limitations. For instance, UMAP can struggle with datasets containing highly complex structures or those with significant noise. Additionally, interpreting the reduced dimensions can be challenging, requiring careful consideration of the original data and the chosen parameters.

Q: How does UMAP compare to other dimensionality reduction techniques?

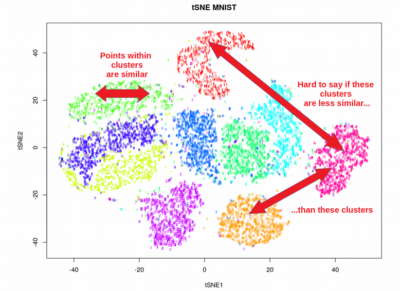
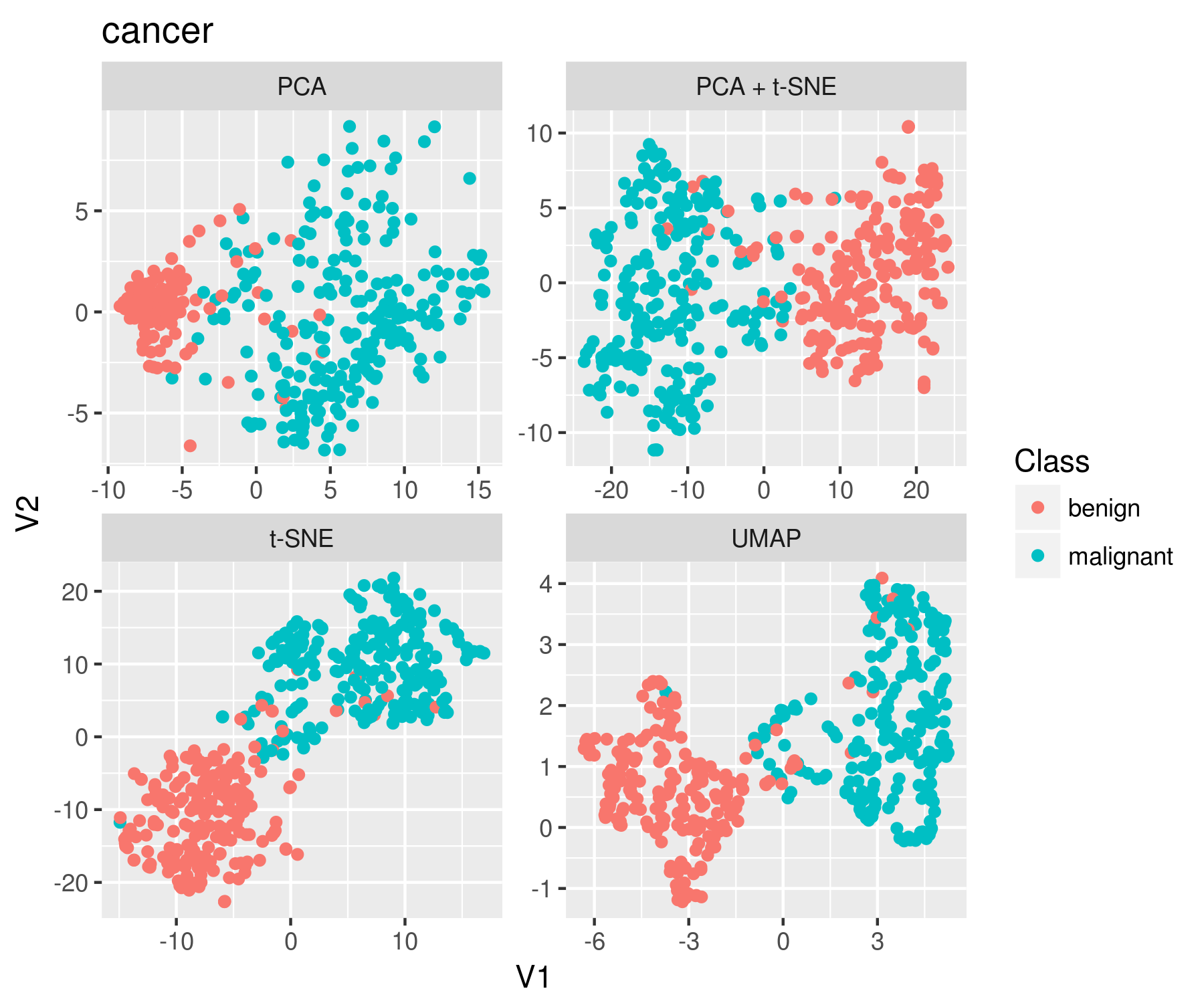
A: UMAP offers distinct advantages over traditional methods like Principal Component Analysis (PCA) and t-SNE. PCA, a linear method, is limited in its ability to capture non-linear relationships, while t-SNE often suffers from issues with scalability and the tendency to cluster points too tightly. UMAP addresses these limitations, providing a more robust and versatile approach.

Q: Can UMAP be used for unsupervised learning tasks?

A: Yes, UMAP is particularly well-suited for unsupervised learning tasks, such as clustering and anomaly detection. By revealing hidden structures and patterns within the data, UMAP enables the identification of distinct groups or outliers that might otherwise be obscured.

Q: Is UMAP suitable for high-dimensional data?

A: UMAP excels at handling high-dimensional data, effectively reducing the dimensionality while preserving the essential structure. Its efficiency and scalability make it a valuable tool for analyzing large datasets with numerous features.

Tips for Successful UMAP Implementation

• Experiment with Parameters: Explore different parameter settings to find the optimal configuration for your specific dataset and analysis goals.

• Visualize the Results: Create visualizations of the reduced data to gain insights into the underlying structure and relationships.

• Consider Data Scaling: Scaling the data before applying UMAP can improve performance and ensure that features with different scales have equal influence.

• Utilize Domain Knowledge: Incorporate domain knowledge to interpret the reduced dimensions and draw meaningful conclusions.

Conclusion: Embracing the Power of UMAP in Data Exploration

UMAP has emerged as a transformative tool in the field of dimensionality reduction, offering a powerful and efficient means to simplify complex datasets while preserving their inherent structure. Its ability to capture both global and local relationships, coupled with its ease of use and scalability, makes it an invaluable asset for data scientists, researchers, and analysts alike. By understanding the principles behind UMAP, its benefits, and the practical steps for its implementation, you can unlock its potential to uncover hidden patterns, gain deeper insights, and make informed decisions based on complex data. As the realm of data science continues to evolve, UMAP stands as a testament to the ingenuity and power of dimensionality reduction techniques, empowering us to navigate the vast landscape of information with clarity and precision.

Closure

Thus, we hope this article has provided valuable insights into Navigating the Landscape of Dimensionality Reduction: A Guide to Installing and Utilizing UMAP in Python. We thank you for taking the time to read this article. See you in our next article!