Mapping The World: A Guide To Map Projections

Mapping the World: A Guide to Map Projections

Related Articles: Mapping the World: A Guide to Map Projections

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Mapping the World: A Guide to Map Projections. Let’s weave interesting information and offer fresh perspectives to the readers.

Mapping the World: A Guide to Map Projections

The Earth, a sphere, presents a challenge when attempting to represent it on a flat surface. This challenge necessitates the use of map projections, mathematical transformations that convert the Earth’s curved surface onto a plane. Each projection introduces distortions, inevitably affecting the representation of size, shape, distance, and direction. Understanding these distortions and the characteristics of different projections is crucial for accurately interpreting maps and selecting the most appropriate projection for specific purposes.

Types of Map Projections

Map projections are broadly categorized based on their preservation properties, the geographic qualities they prioritize at the expense of others. The three main categories are:

1. Conformal Projections:

Conformal projections maintain the correct angles and shapes of small features, such as the coastline or islands, at the expense of distorting area. This makes them ideal for navigation and applications requiring accurate local measurements.

a) Mercator Projection:

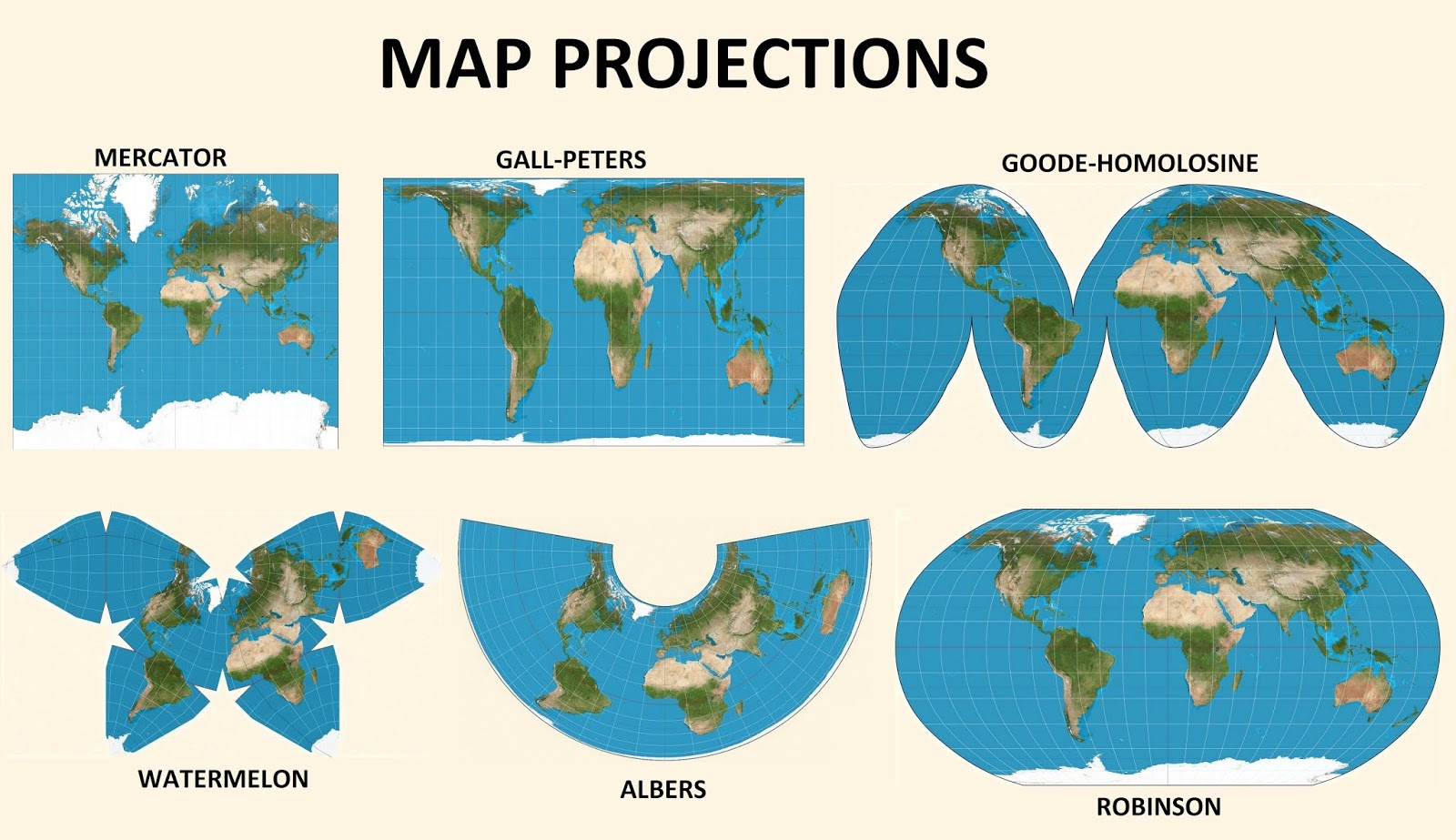
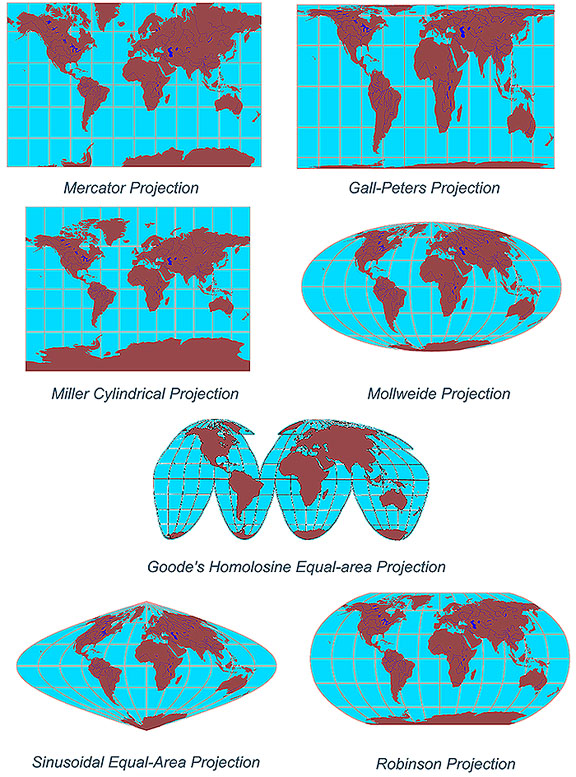
The most widely recognized conformal projection, the Mercator projection, is a cylindrical projection that stretches areas further from the equator, resulting in significant exaggeration of landmasses near the poles. While it maintains accurate shapes, it distorts the true size of regions, particularly at higher latitudes. Despite this distortion, its straight lines representing constant compass bearings make it invaluable for navigation.

b) Transverse Mercator Projection:

A variation of the Mercator projection, the Transverse Mercator projection, rotates the cylinder to align with a meridian, making it ideal for mapping long, narrow areas like countries or continents. This projection is often used for creating large-scale maps of regions extending along a single meridian.

c) Lambert Conformal Conic Projection:

This conic projection uses a cone intersecting the Earth at two parallels, minimizing distortion within a defined zone. It is widely used for mapping large areas with moderate east-west extents, such as the United States.

2. Equal-Area Projections:

Equal-area projections prioritize the accurate representation of area, ensuring that the relative sizes of landmasses are preserved. However, they compromise shape, often distorting the shapes of continents and countries. These projections are useful for comparative studies, population density mapping, and resource distribution analysis.

a) Albers Equal-Area Conic Projection:

A popular equal-area projection, the Albers projection, uses a cone intersecting the Earth at two parallels. It provides accurate area representation within a defined zone and is often used for mapping large regions like the United States.

b) Lambert Azimuthal Equal-Area Projection:

This azimuthal projection preserves area by projecting the Earth onto a plane tangent to a specific point. It is commonly used for mapping polar regions and for visualizing global data.

c) Mollweide Projection:

A pseudo-cylindrical projection, the Mollweide projection, maintains area while distorting shapes, particularly near the poles. Its oval shape and uniform distribution of landmasses make it suitable for displaying global data.

3. Equidistant Projections:

Equidistant projections prioritize accurate distances from a specific point, typically a central meridian or a pole. While they preserve distance, they distort both shape and area. These projections are useful for measuring distances from a central point and for navigational purposes.

a) Azimuthal Equidistant Projection:

This azimuthal projection preserves distances from a central point. It is often used for mapping polar regions and for visualizing distances from a specific location.

b) Plate Carrée Projection:

Also known as the Equirectangular projection, this simple projection preserves distances along the equator and central meridian. It is often used for basic world maps and for displaying data with uniform spatial distribution.

c) Sinusoidal Projection:

This projection preserves distances along the central meridian and the equator. It is often used for mapping the Earth’s surface and for visualizing global data.

Frequently Asked Questions (FAQs)

1. What is the best map projection for a world map?

There is no single "best" projection for a world map, as each projection prioritizes different properties. The choice depends on the intended use of the map. For general-purpose maps, the Mollweide projection offers a good balance between area accuracy and visual appeal. For navigation, the Mercator projection is preferred, despite its area distortion.

2. Why do map projections distort the Earth’s surface?

Map projections distort the Earth’s surface because it is impossible to accurately represent a sphere on a flat plane without introducing some form of distortion. Each projection prioritizes specific properties, inevitably compromising others.

3. How can I choose the right map projection for my needs?

Consider the purpose of the map and the data it will display. If you need to represent accurate shapes, choose a conformal projection. If area accuracy is paramount, select an equal-area projection. If distances from a specific point are crucial, opt for an equidistant projection.

4. Are there any limitations to map projections?

All map projections introduce distortions, and no single projection can perfectly represent the Earth’s surface. The choice of projection should be made carefully, considering the intended use and the specific distortions it introduces.

Tips for Selecting a Map Projection

1. Consider the intended use: What is the map being used for? Navigation, data visualization, or general-purpose mapping?
2. Identify the geographic region: Is the map for a local area, a country, or the entire globe?
3. Determine the priority: Which properties are most important for the map’s purpose: shape, area, or distance?
4. Research different projections: Compare the characteristics and distortions of various projections to find the most suitable one.

Conclusion

Map projections are essential tools for representing the Earth’s curved surface on a flat plane. Each projection introduces distortions, but by understanding the characteristics of different projections and their preservation properties, users can select the most appropriate projection for their specific needs. Choosing the right projection ensures accurate representation of data and facilitates effective communication and analysis.

Closure

Thus, we hope this article has provided valuable insights into Mapping the World: A Guide to Map Projections. We thank you for taking the time to read this article. See you in our next article!