Mapping the World: A Comprehensive Guide to Conformal Map Projections
Related Articles: Mapping the World: A Comprehensive Guide to Conformal Map Projections
Introduction
With enthusiasm, let’s navigate through the intriguing topic related to Mapping the World: A Comprehensive Guide to Conformal Map Projections. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
Mapping the World: A Comprehensive Guide to Conformal Map Projections

The Earth, a sphere suspended in space, presents a unique challenge for cartographers. Representing this curved surface on a flat map necessitates the use of projections, mathematical transformations that distort the Earth’s geometry to fit a two-dimensional plane. Among these projections, conformal maps stand out for their ability to preserve angles, making them valuable tools for navigation, surveying, and various scientific applications.
Understanding Conformal Projections
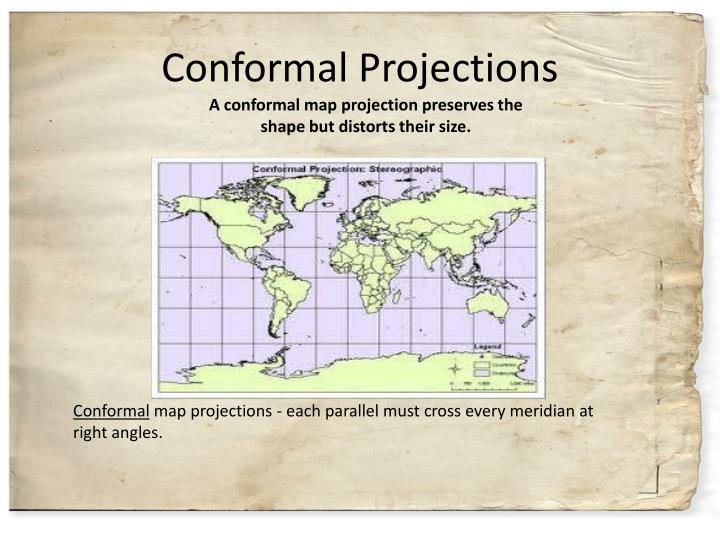
Conformal projections, also known as orthomorphic projections, prioritize the accurate representation of angles at the expense of area and distance. This means that while shapes are preserved locally, their sizes and distances may be distorted. However, the preservation of angles ensures that the relative directions between points on the map accurately reflect their real-world counterparts.
Key Characteristics of Conformal Projections:
- Angle Preservation: The most defining feature of conformal projections is their ability to accurately depict angles. This is crucial for navigation, where precise bearings and directions are essential.
- Shape Preservation (Locally): While areas and distances are distorted, conformal projections maintain the shapes of small features, such as islands or cities, in their immediate vicinity.
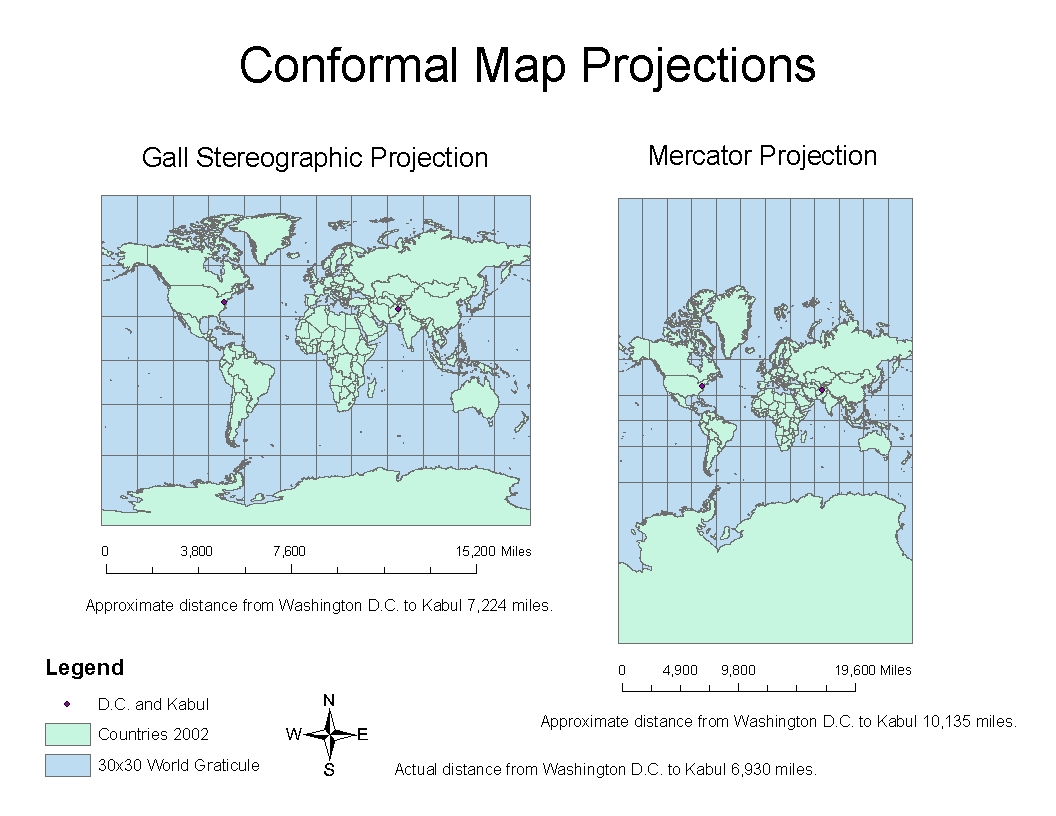
- Mercator Projection: A Notable Example: The Mercator projection, perhaps the most widely recognized conformal projection, is famous for its rectangular grid and its ability to maintain accurate compass bearings. However, it significantly distorts areas, particularly towards the poles.
Types of Conformal Projections:
Conformal projections are classified based on their specific properties and the distortions they introduce. Some common types include:
- Cylindrical Projections: These projections wrap a cylinder around the Earth, creating a rectangular map. Examples include the Mercator projection and the Transverse Mercator projection.
- Conic Projections: These projections use a cone to project the Earth’s surface, resulting in maps with curved edges. Examples include the Lambert Conformal Conic projection and the Albers Equal-Area Conic projection.
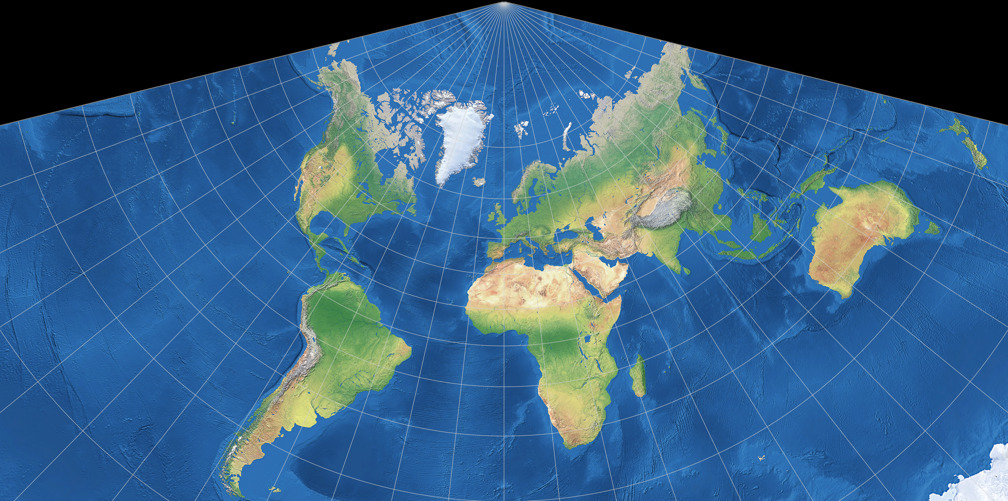
- Azimuthal Projections: These projections project the Earth’s surface onto a plane tangent to a specific point, creating circular maps. Examples include the Stereographic projection and the Gnomonic projection.
Applications of Conformal Projections:
Conformal projections find widespread use in various fields:
- Navigation: The preservation of angles in conformal projections makes them ideal for maritime and aviation navigation, where accurate bearings and directions are paramount.
- Surveying and Mapping: Conformal projections are crucial for creating accurate maps and charts used in land surveying, urban planning, and resource management.
- Meteorology and Oceanography: These projections are used in weather forecasting and oceanographic studies to accurately represent atmospheric and oceanic patterns.
- Geographical Information Systems (GIS): Conformal projections play a significant role in GIS applications, enabling the accurate display and analysis of spatial data.
Advantages and Disadvantages of Conformal Projections:
Advantages:
- Accurate Angle Representation: Conformal projections preserve angles, crucial for navigation, surveying, and other applications requiring precise directions.
- Shape Preservation (Locally): The accurate depiction of shapes within small areas makes them suitable for detailed maps of cities, islands, or other features.
Disadvantages:
- Area Distortion: Conformal projections significantly distort areas, especially towards the poles. This can lead to misinterpretations regarding the size of landmasses or oceans.
- Distance Distortion: Distances are also distorted, particularly near the poles and along lines of longitude. This can create inaccuracies in measuring distances between points on the map.
FAQs on Conformal Projections:
Q: What is the difference between conformal and equal-area projections?
A: While conformal projections prioritize angle preservation, equal-area projections prioritize area preservation. This means that conformal maps accurately depict shapes but distort areas, while equal-area maps accurately depict areas but distort shapes.
Q: Why is the Mercator projection so popular despite its distortions?
A: The Mercator projection’s popularity stems from its ability to maintain accurate compass bearings and its rectangular grid, which is easy to use for navigation and mapmaking. However, its significant area distortion, particularly near the poles, is a major drawback.
Q: Are there any alternatives to conformal projections for specific applications?
A: Yes, depending on the application, other types of projections may be more suitable. For example, equal-area projections are better for representing the true relative sizes of landmasses, while equidistant projections are ideal for accurately depicting distances from a central point.
Q: How do I choose the right conformal projection for my needs?
A: Selecting the appropriate conformal projection depends on the specific application and the geographical area of interest. Factors to consider include the desired level of accuracy for angles, the acceptable level of area distortion, and the shape and size of the region being mapped.
Tips for Using Conformal Projections:
- Understand the Distortions: Be aware of the distortions inherent in conformal projections, particularly regarding area and distance.
- Use Appropriate Projections for Specific Applications: Select the projection that best suits the specific needs of the application, considering factors such as navigation, surveying, or analysis.
- Consult with Experts: If you are unsure about which conformal projection to use, consult with cartographers or GIS specialists for expert advice.
Conclusion:
Conformal projections are essential tools for representing the Earth’s surface on flat maps, enabling accurate angle preservation and local shape preservation. Their widespread use in navigation, surveying, and various scientific applications underscores their importance. However, understanding the inherent distortions in these projections is crucial for interpreting and using maps effectively. By carefully considering the specific needs of an application and the limitations of conformal projections, users can harness their power for accurate and informative mapmaking.
![]()




Closure
Thus, we hope this article has provided valuable insights into Mapping the World: A Comprehensive Guide to Conformal Map Projections. We appreciate your attention to our article. See you in our next article!