MAPE: A Comprehensive Guide To Evaluating Model Performance

MAPE: A Comprehensive Guide to Evaluating Model Performance

Related Articles: MAPE: A Comprehensive Guide to Evaluating Model Performance

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to MAPE: A Comprehensive Guide to Evaluating Model Performance. Let’s weave interesting information and offer fresh perspectives to the readers.

MAPE: A Comprehensive Guide to Evaluating Model Performance

In the realm of machine learning, evaluating the performance of a model is crucial for determining its effectiveness and reliability. While various metrics exist to assess model accuracy, the Mean Absolute Percentage Error (MAPE) stands out as a widely used and intuitive measure. This article delves into the intricacies of MAPE, exploring its definition, calculation, advantages, limitations, and practical applications.

Understanding MAPE: A Measure of Prediction Accuracy

MAPE quantifies the average percentage error between predicted values and actual values. It provides a clear and interpretable measure of how well a model is able to predict future outcomes. Unlike other metrics that focus on absolute errors, MAPE considers the relative error, making it particularly useful for scenarios where the scale of the data is significant.

Calculating MAPE: A Step-by-Step Guide

The calculation of MAPE involves the following steps:

1. Determine the absolute errors: For each data point, calculate the absolute difference between the predicted value and the actual value.
2. Divide by the actual values: Divide each absolute error by the corresponding actual value.
3. Calculate the average percentage error: Sum all the percentage errors and divide by the total number of data points.

Mathematically, MAPE can be represented as:

MAPE = (1/n) * Σ(|Actual Value - Predicted Value| / |Actual Value|) * 100

Where:

• n: Number of data points
• Σ: Summation symbol

Advantages of MAPE: A Clear and Interpretable Metric

MAPE offers several advantages that make it a valuable tool for model evaluation:

• Intuitive interpretation: MAPE expresses errors as percentages, making it easy to understand the magnitude of the prediction errors. A MAPE of 5% indicates that, on average, the model’s predictions are off by 5%.
• Scale-independent: MAPE is not affected by the scale of the data, making it suitable for comparing models trained on datasets with different units or magnitudes.
• Focus on relative error: MAPE emphasizes the relative error, providing a more meaningful measure of accuracy when dealing with large values.

Limitations of MAPE: Potential Drawbacks and Alternatives

While MAPE offers several advantages, it also has certain limitations that should be considered:

• Sensitivity to outliers: MAPE is highly sensitive to outliers, as a single large error can significantly inflate the overall percentage error.
• Zero values: MAPE cannot be calculated when the actual value is zero, as it would result in division by zero.
• Potential for misleading results: In cases where the actual values are close to zero, MAPE can provide misleading results, as even small absolute errors can lead to large percentage errors.

In cases where MAPE’s limitations are a concern, alternative metrics like Root Mean Squared Error (RMSE) or Mean Absolute Error (MAE) might be more appropriate.

Applications of MAPE: Real-World Scenarios

MAPE finds application in various domains where accurate predictions are crucial:

• Financial forecasting: Evaluating the accuracy of financial models for predicting stock prices, interest rates, or economic growth.
• Sales forecasting: Assessing the performance of models used to predict sales revenue or demand for products.
• Inventory management: Evaluating the accuracy of models used to predict inventory levels and optimize stock replenishment.
• Healthcare: Evaluating the accuracy of models used to predict patient outcomes or disease progression.

FAQs Regarding MAPE: Addressing Common Questions

1. What is the ideal MAPE value?

The ideal MAPE value depends on the specific application and acceptable error tolerance. Generally, a lower MAPE indicates higher accuracy. However, the acceptable range can vary significantly depending on the context.

2. How can I improve the MAPE of my model?

Improving MAPE typically involves refining the model itself or the data used for training. Techniques like feature engineering, hyperparameter tuning, or using more sophisticated algorithms can enhance model performance.

3. Can MAPE be negative?

No, MAPE cannot be negative. It represents the average percentage error, which is always a positive value.

4. Is MAPE a good measure for all models?

While MAPE is a widely used metric, it might not be suitable for all models. The choice of evaluation metric should be based on the specific application and the nature of the data.

Tips for Utilizing MAPE Effectively: Practical Recommendations

• Consider the context: Understand the specific application and the acceptable error tolerance before interpreting MAPE results.
• Explore alternative metrics: Investigate other metrics like RMSE or MAE to gain a more comprehensive understanding of model performance.
• Address outliers: Identify and address outliers in the data to mitigate their impact on MAPE.
• Monitor MAPE over time: Track MAPE performance over time to identify trends and areas for improvement.

Conclusion: A Powerful Tool for Model Evaluation

MAPE is a valuable tool for evaluating the performance of machine learning models, offering a clear and interpretable measure of prediction accuracy. Its intuitive nature and scale-independent properties make it widely applicable across various domains. While MAPE has its limitations, understanding its strengths and weaknesses allows for informed decision-making regarding model selection and improvement. By utilizing MAPE effectively, practitioners can gain deeper insights into model performance and optimize their decision-making processes.

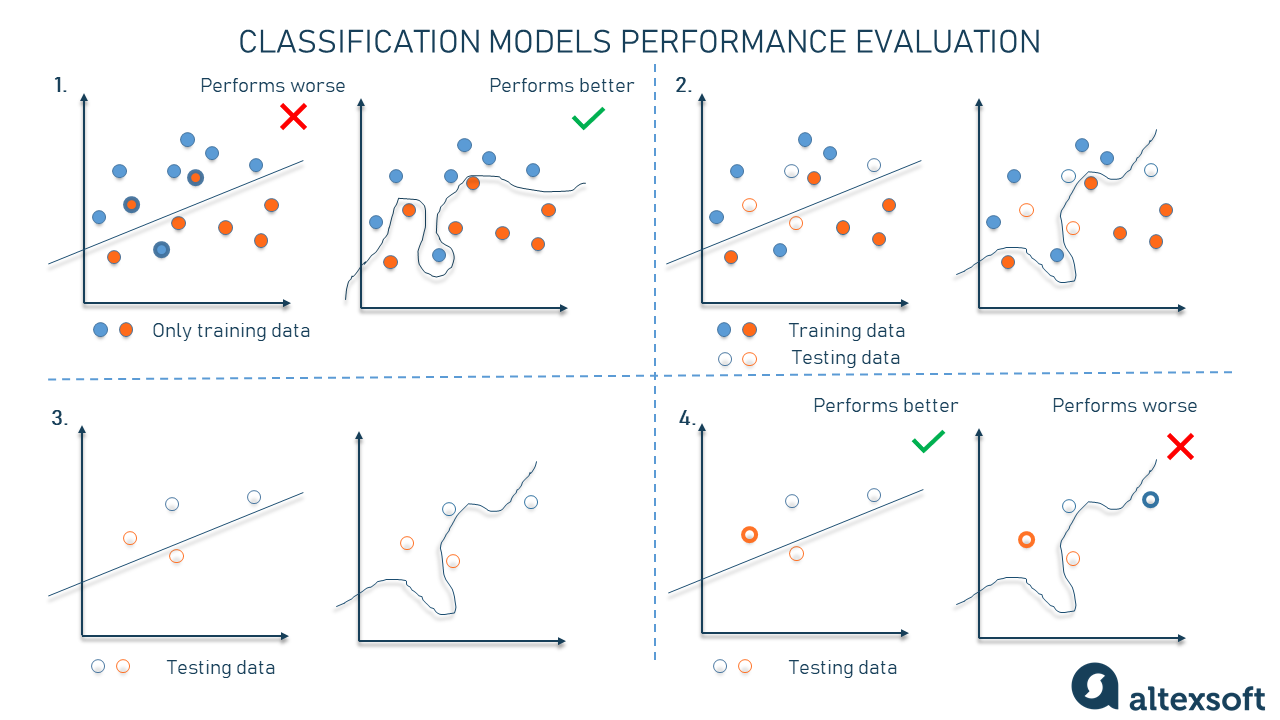
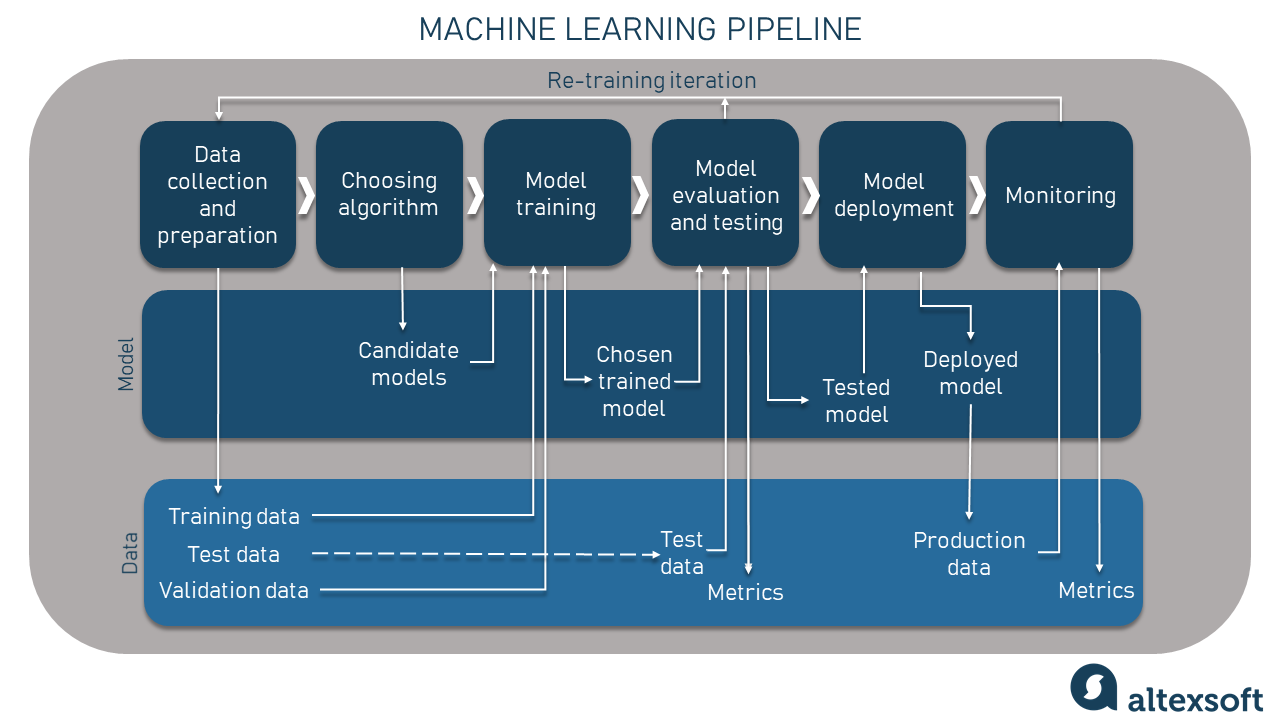
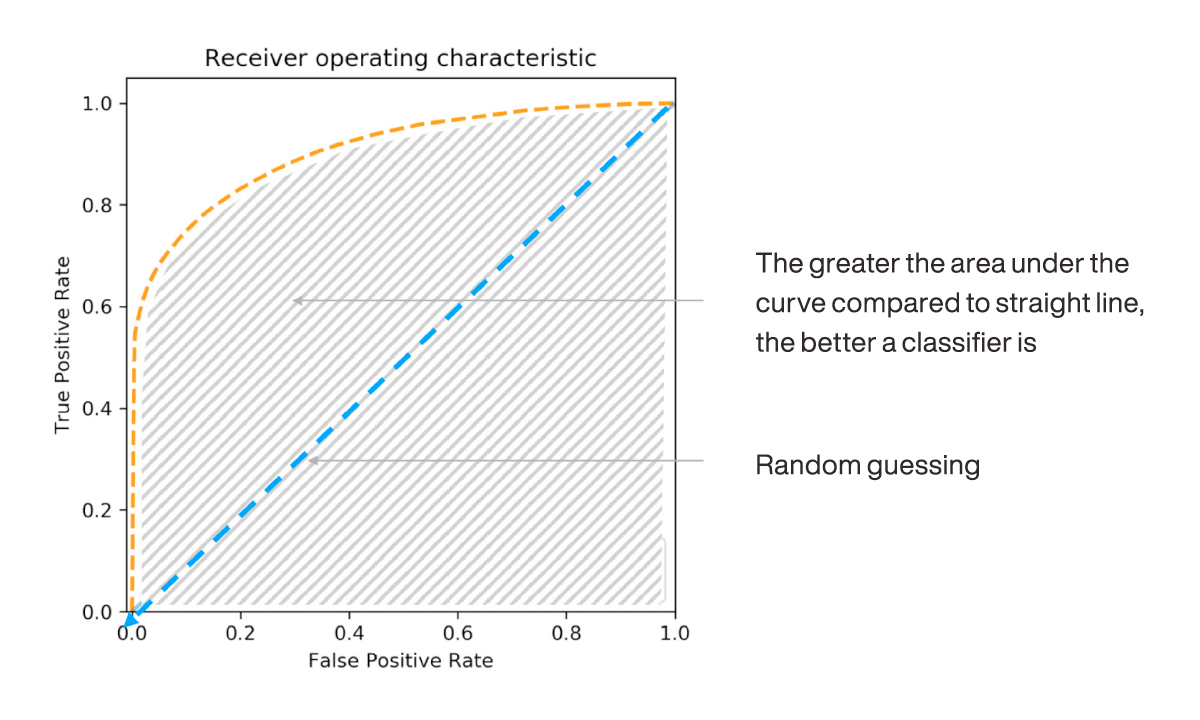
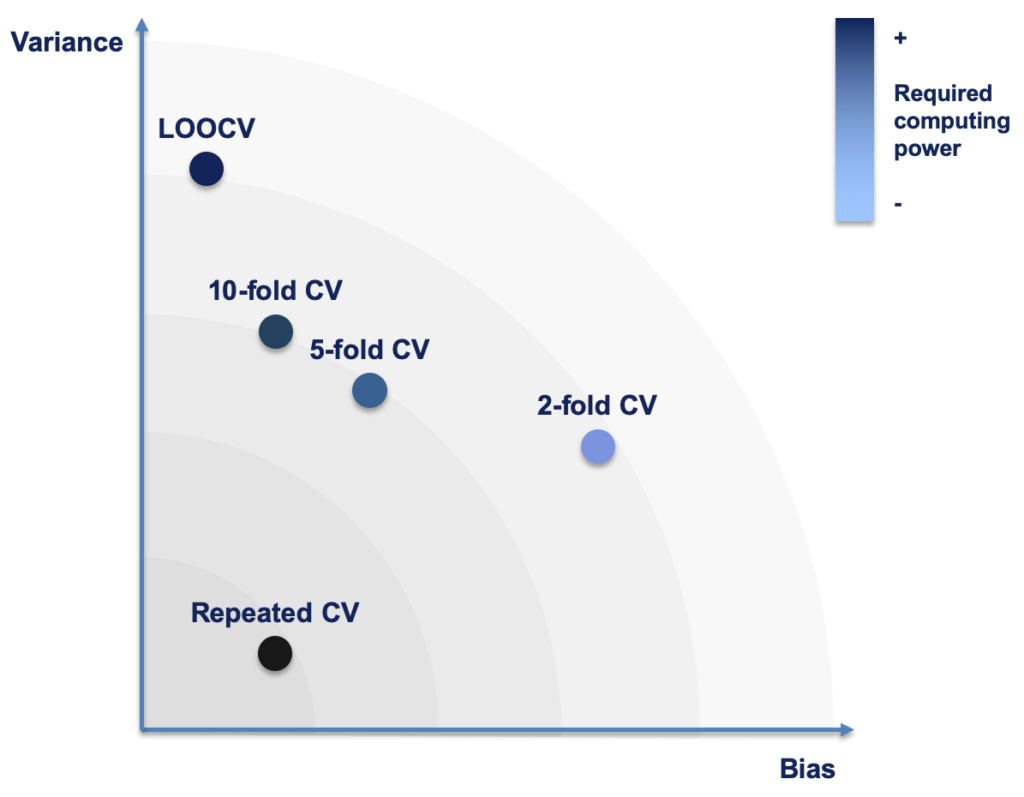
Closure

Thus, we hope this article has provided valuable insights into MAPE: A Comprehensive Guide to Evaluating Model Performance. We appreciate your attention to our article. See you in our next article!