Demystifying Boolean Logic: A Comprehensive Guide To Karnaugh Map Solvers In Python

Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Map Solvers in Python

Related Articles: Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Map Solvers in Python

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Map Solvers in Python. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Map Solvers in Python

Boolean algebra, the foundation of digital circuits and computer science, deals with logical operations on binary values (0 and 1). Simplifying Boolean expressions is crucial for designing efficient and cost-effective circuits. While traditional algebraic methods can be cumbersome, Karnaugh maps provide a visual and intuitive approach to simplification. This article delves into the world of Karnaugh map solvers in Python, exploring their significance, functionalities, and practical applications.

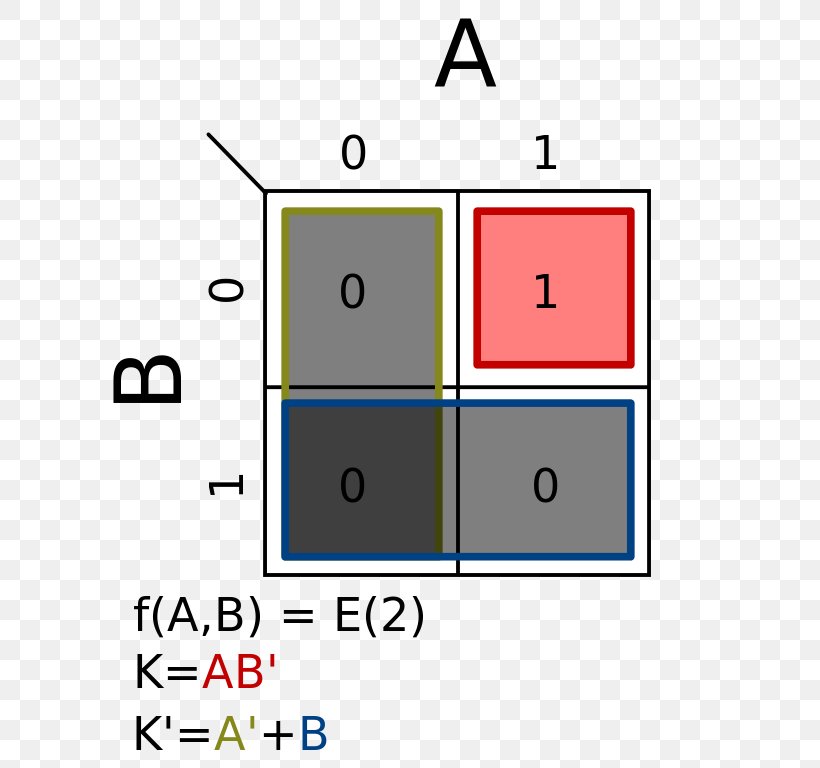
Understanding Karnaugh Maps

A Karnaugh map, also known as a K-map, is a graphical representation of a truth table for a Boolean function. It arranges the input combinations in a grid format, where each cell represents a unique combination of input variables. The map’s structure ensures that adjacent cells differ by only one input variable, facilitating the identification of groups of adjacent cells with the same output value.

Key Features of Karnaugh Maps:

• Visual Representation: K-maps provide a visual representation of the Boolean function, making it easier to understand the relationships between input variables and the output.
• Simplified Expression: By grouping adjacent cells with the same output value, K-maps enable the identification of common factors, leading to simplified Boolean expressions.
• Minimized Logic Circuits: Simplified expressions translate to smaller and more efficient logic circuits, reducing the number of gates required and lowering the overall cost.

Python: A Powerful Tool for Karnaugh Map Manipulation

Python, with its vast libraries and intuitive syntax, offers a versatile platform for implementing Karnaugh map solvers. These solvers automate the simplification process, reducing the manual effort required and minimizing the possibility of errors.

Exploring the Anatomy of a Python Karnaugh Map Solver

A typical Python Karnaugh map solver comprises several key components:

1. Input Representation: The solver first needs to receive the Boolean function as input. This can be done in various ways:

   • Truth Table: The function can be defined by providing a truth table, listing all possible input combinations and their corresponding output values.
   • Boolean Expression: The function can be directly input as a string containing the Boolean expression.
   • Minterm List: The function can be represented as a list of minterms, where each minterm corresponds to an input combination that produces a ‘1’ output.

2. Map Generation: Based on the input representation, the solver constructs a Karnaugh map. This involves:

   • Determining the Map Size: The number of rows and columns in the map depends on the number of input variables. A map with ‘n’ input variables will have 2^n cells.
   • Arranging Cells: The cells are arranged in a specific order, ensuring that adjacent cells differ by only one input variable. This arrangement is crucial for identifying groups of adjacent cells with the same output value.

3. Grouping and Simplification: The solver then identifies groups of adjacent cells with the same output value. These groups are called "prime implicants." The solver aims to find the smallest possible number of prime implicants that cover all the cells with a ‘1’ output.

   • Grouping Rules: The solver uses specific rules to group cells:
     • Cells can be grouped horizontally or vertically.
     • Groups can contain 2^n cells, where ‘n’ is an integer.
     • Groups can wrap around the edges of the map.

4. Expression Generation: Once the prime implicants are identified, the solver generates a simplified Boolean expression from them. This involves:

   • Identifying Essential Prime Implicants: Some prime implicants are essential, meaning they cover a cell that cannot be covered by any other prime implicant. These must be included in the simplified expression.
   • Selecting Non-Essential Prime Implicants: The solver then selects non-essential prime implicants to cover the remaining cells, prioritizing those that cover the largest number of cells.

5. Output Generation: Finally, the solver presents the simplified Boolean expression as the output, representing the minimized form of the original function.

Python Libraries for Karnaugh Map Solving

Several Python libraries simplify the development of Karnaugh map solvers:

• KarnaughMap: A dedicated library specifically designed for solving Karnaugh maps. It provides functions for creating, manipulating, and simplifying maps.
• NumPy: A powerful library for numerical computing, which can be used to represent and manipulate the Karnaugh map grid.
• SciPy: A scientific computing library that offers optimization algorithms that can be applied to finding the optimal set of prime implicants.

Practical Applications of Karnaugh Map Solvers

Karnaugh map solvers find applications in various domains:

• Digital Circuit Design: Simplifying Boolean expressions leads to smaller and more efficient logic circuits, reducing the number of gates and minimizing cost.
• Computer Science: Understanding and manipulating Boolean functions is fundamental to various computer science concepts, including digital logic, data structures, and algorithms.
• Education: K-map solvers can be used as educational tools to teach Boolean algebra and logic circuit design concepts.

Benefits of Using Python Karnaugh Map Solvers

• Automation: Python solvers automate the simplification process, reducing manual effort and minimizing the chance of errors.
• Efficiency: The solvers identify the smallest possible set of prime implicants, leading to highly optimized Boolean expressions.
• Versatility: Python solvers can handle Boolean functions of various complexities, with a wide range of input representations.
• User-Friendliness: Python’s intuitive syntax and libraries make it easy to develop and use Karnaugh map solvers.

FAQs on Karnaugh Map Solvers in Python

Q1: What are the limitations of Karnaugh maps?

• Complexity: As the number of input variables increases, the size of the Karnaugh map grows exponentially, making it difficult to visualize and manipulate.
• Non-Standard Functions: K-maps are not suitable for simplifying Boolean functions with non-standard forms, such as those involving XOR or XNOR operations.

Q2: How can I choose the right Python library for my Karnaugh map solver?

• KarnaughMap: Ideal for basic K-map solving, offering dedicated functions for map manipulation and simplification.
• NumPy: Provides powerful array manipulation capabilities for representing and processing the map grid.
• SciPy: Offers optimization algorithms that can be used to find the optimal set of prime implicants.

Q3: Can I use Karnaugh maps for functions with more than four input variables?

• While K-maps are traditionally used for functions with up to four variables, techniques like "map folding" can be applied to handle functions with more variables. However, for functions with a large number of inputs, other simplification methods, such as Quine-McCluskey, might be more efficient.

Q4: Are there any alternative methods for Boolean expression simplification?

• Quine-McCluskey Algorithm: A tabular method for simplifying Boolean expressions, particularly useful for functions with a large number of input variables.
• Espresso Algorithm: An automated method that uses a combination of tabular and heuristic techniques for efficient simplification.

Tips for Using Python Karnaugh Map Solvers

• Start with Simple Examples: Begin by working with small and straightforward Boolean functions to understand the basics of K-maps and Python solvers.
• Visualize the Map: Use graphical representations of the Karnaugh map to aid in understanding the simplification process.
• Explore Different Libraries: Experiment with different Python libraries to find the best fit for your needs and coding style.
• Compare with Algebraic Methods: Use traditional algebraic methods to verify the results obtained by the Python solver.

Conclusion

Karnaugh map solvers in Python provide a powerful and intuitive approach to simplifying Boolean expressions, leading to efficient and cost-effective digital circuit designs. By leveraging the versatility of Python and its libraries, developers can automate the simplification process, minimize errors, and optimize their circuit designs. While K-maps have limitations, particularly with a large number of input variables, they remain a valuable tool for understanding and manipulating Boolean functions, serving as a foundation for further exploration of more advanced simplification methods.

Closure

Thus, we hope this article has provided valuable insights into Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Map Solvers in Python. We thank you for taking the time to read this article. See you in our next article!