Conformal Map Projections: Preserving Shapes and Angles in a Flattened World
Related Articles: Conformal Map Projections: Preserving Shapes and Angles in a Flattened World
Introduction
With great pleasure, we will explore the intriguing topic related to Conformal Map Projections: Preserving Shapes and Angles in a Flattened World. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
Conformal Map Projections: Preserving Shapes and Angles in a Flattened World

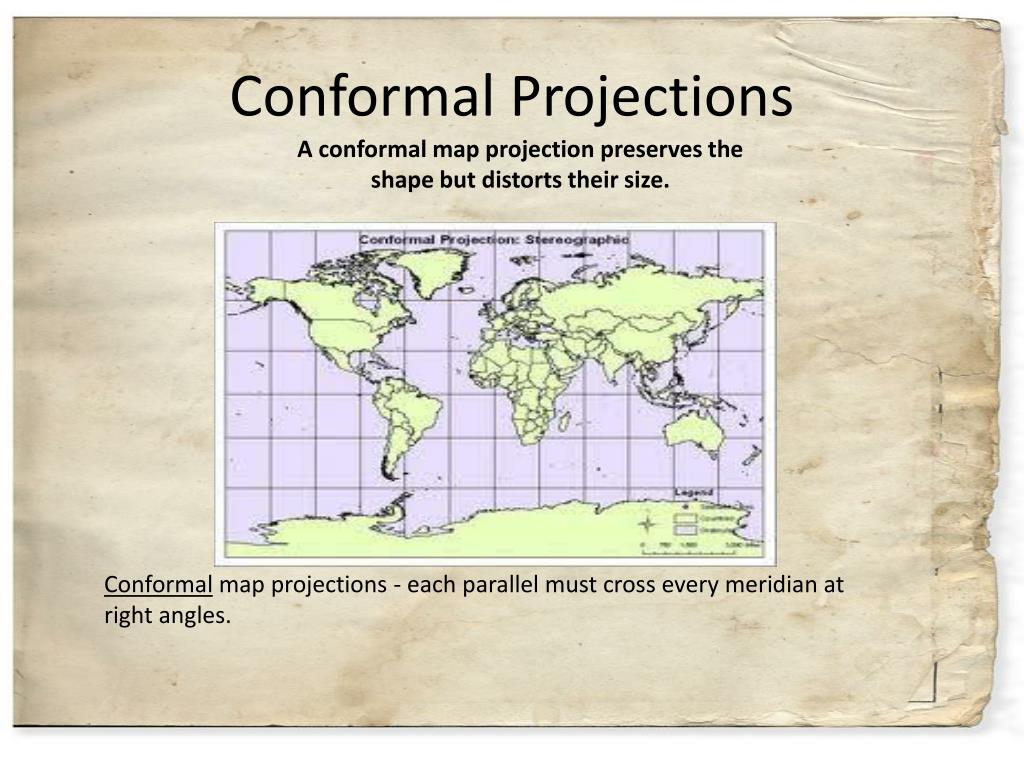
The Earth, a sphere, presents a challenge for cartographers. To represent our planet on a flat map, distortions are inevitable. One crucial aspect of these distortions is the preservation of angles and shapes. This is where conformal map projections come into play.
Conformal projections are a class of map projections that prioritize the accurate representation of angles at the expense of area. This means that shapes on the map will be true to their real-world counterparts, but their sizes may be distorted. While areas might be stretched or compressed, the angles between lines on the map accurately reflect the angles on the Earth’s surface.
This characteristic makes conformal projections ideal for applications where precise angular relationships are paramount. For example, in navigation, where accurate bearings are critical, conformal projections are essential. Similarly, in meteorological applications, where wind patterns and other weather phenomena are analyzed, conformal projections ensure that the direction and intensity of these phenomena are accurately represented.
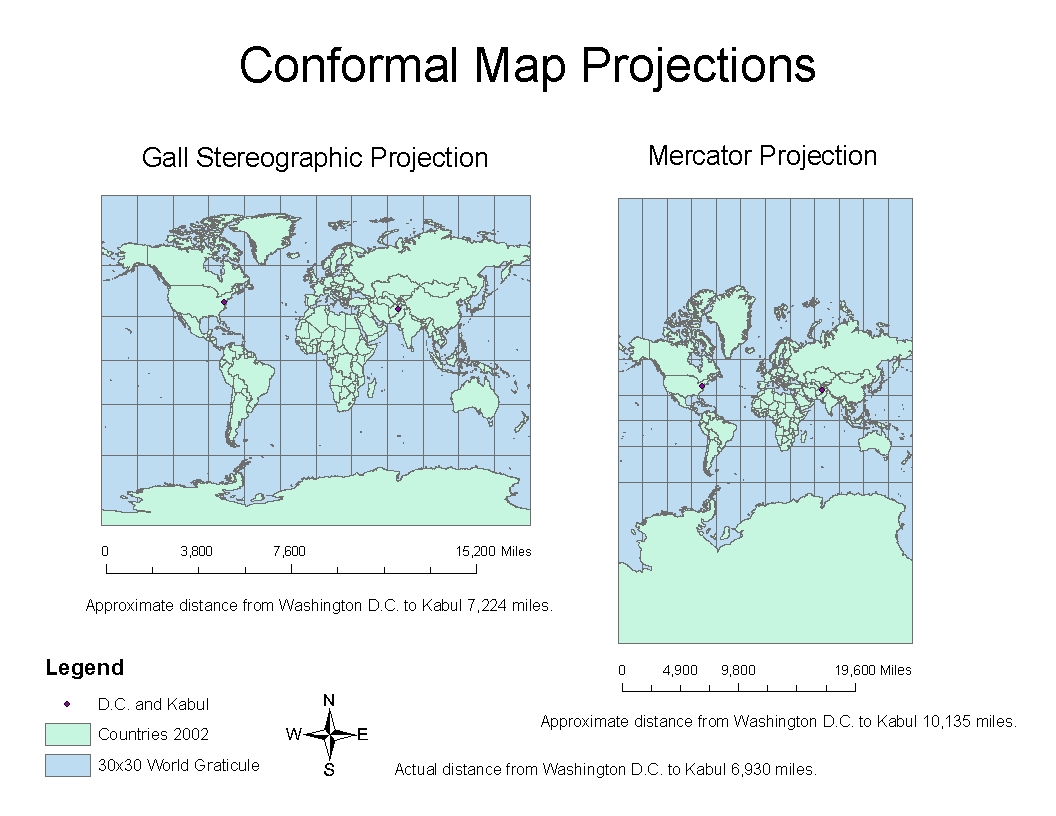
The Mercator Projection: A Conformal Masterpiece
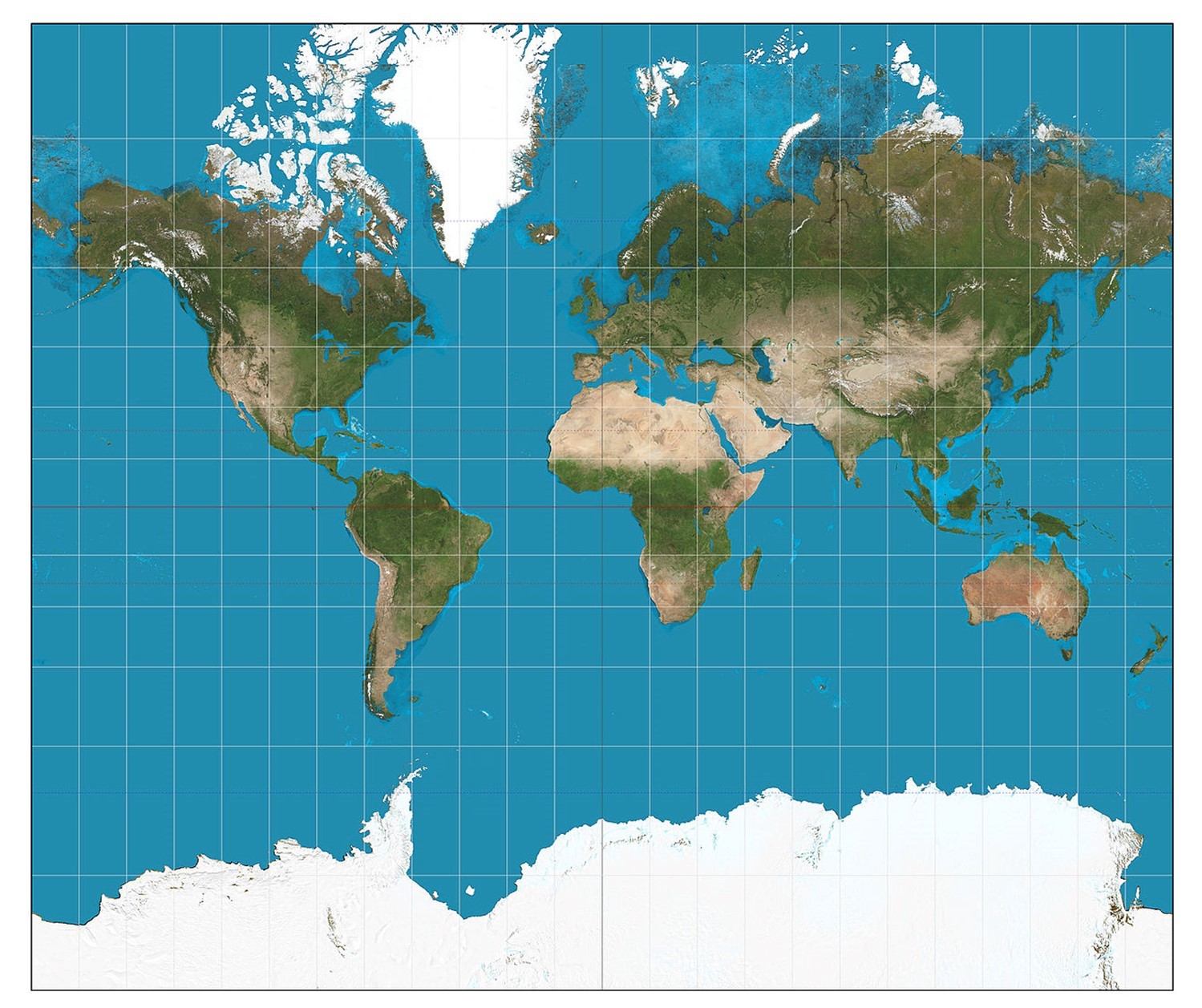
The most widely recognized conformal projection is the Mercator projection. Developed by the Flemish cartographer Gerardus Mercator in 1569, it has become synonymous with world maps. The Mercator projection is a cylindrical projection, meaning it imagines the Earth wrapped in a cylinder. The projection is conformal because it preserves the angles at every point on the map.
However, the Mercator projection suffers from significant distortion in areas far from the equator. As one moves away from the equator towards the poles, the map stretches the landmasses, making high-latitude regions appear much larger than they are in reality.
Beyond the Mercator: Other Conformal Projections
While the Mercator projection is well-known, it is not the only conformal projection available. Several other projections offer unique advantages and are suitable for different applications.
-
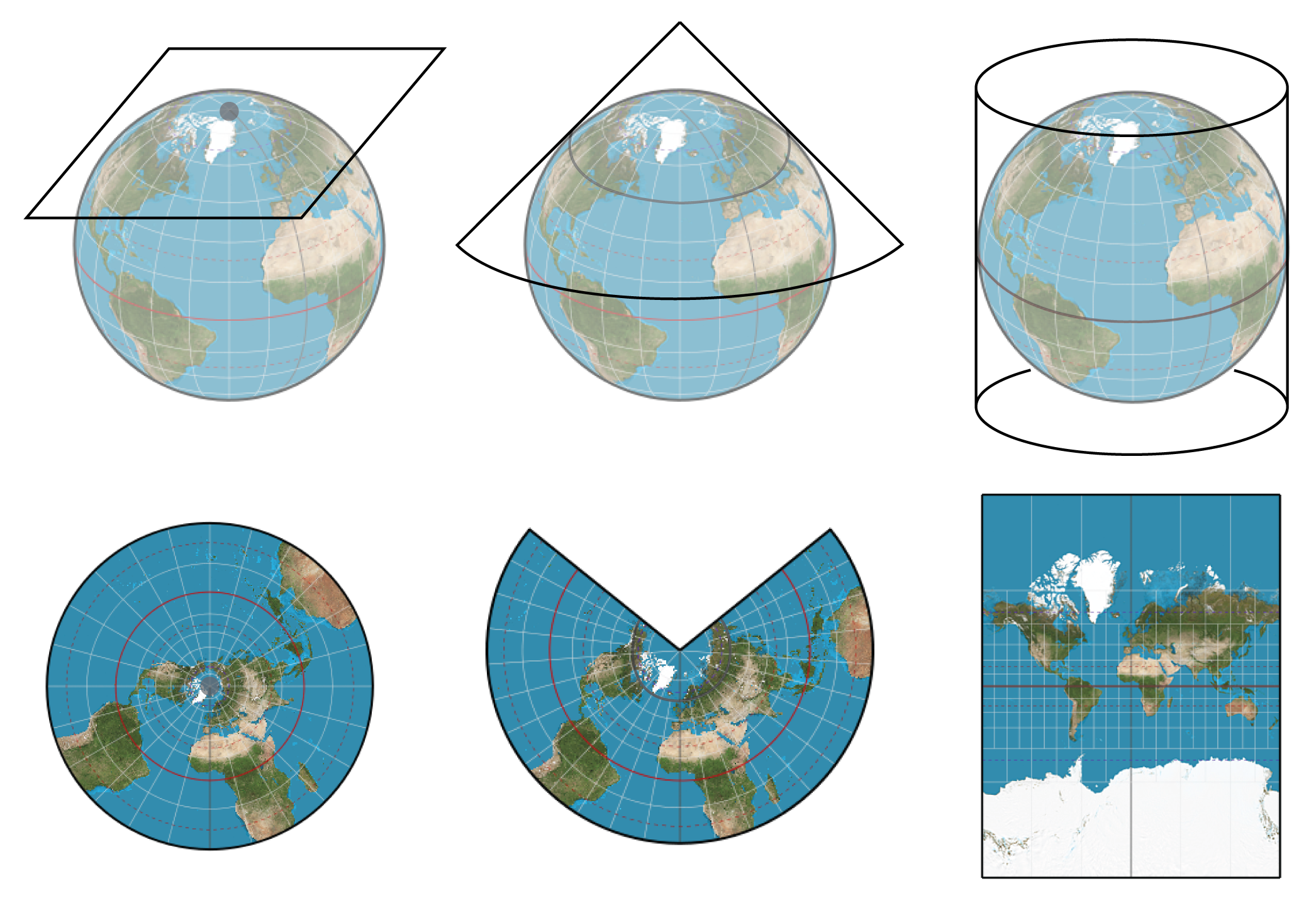
The Transverse Mercator Projection: This projection is similar to the Mercator but rotates the cylinder so that it touches the Earth along a meridian instead of the equator. This makes it ideal for mapping countries or regions that are elongated in a north-south direction.
-
The Lambert Conformal Conic Projection: This projection uses a cone instead of a cylinder to project the Earth’s surface. It is conformal and allows for less distortion in areas further from the equator compared to the Mercator. The Lambert projection is commonly used for mapping large regions, such as continents or countries.
-
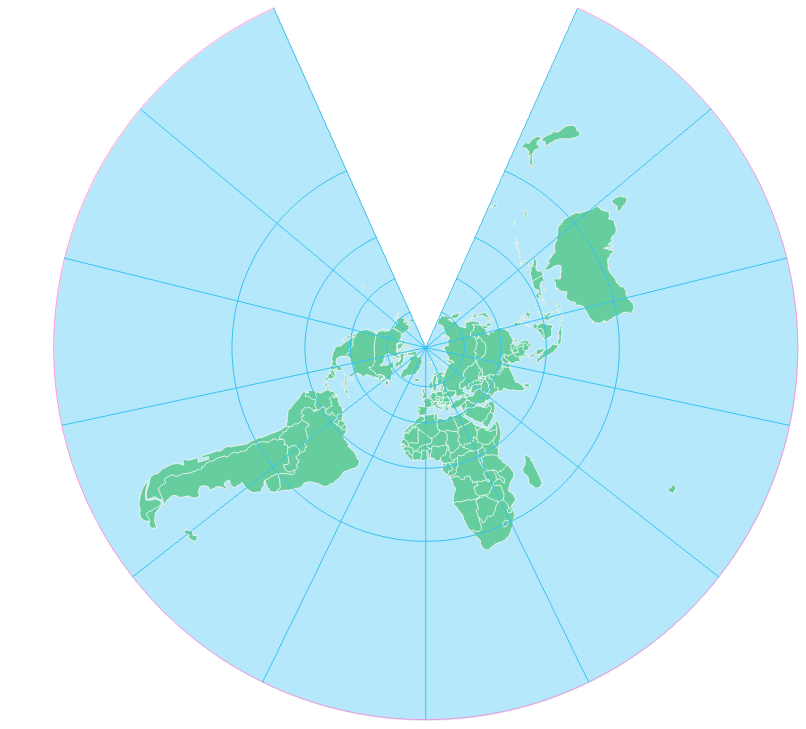
The Stereographic Projection: This projection uses a plane instead of a cylinder or cone. It is conformal and particularly useful for mapping polar regions, as it avoids the extreme distortions that occur in other projections at high latitudes.
Choosing the Right Conformal Projection
The choice of conformal projection depends on the specific application and the region being mapped. Consider the following factors:
-
The area of interest: The size and shape of the region will influence the choice of projection. For instance, the Mercator is suitable for mapping the globe, while the Transverse Mercator is better for narrow, elongated regions.
-
The intended use: The application will determine the level of distortion that can be tolerated. For navigation, accuracy is paramount, while for general mapping, some distortion might be acceptable.
-
The desired projection properties: While conformal projections preserve angles, they may distort area. Consider whether area accuracy is important for the application.
FAQs about Conformal Map Projections
Q: What is the difference between a conformal and an equal-area map projection?
A: Conformal projections preserve angles but distort areas, while equal-area projections preserve areas but distort angles. The choice between the two depends on the specific application and the desired balance between angle and area accuracy.
Q: Why are conformal projections important for navigation?
A: Conformal projections ensure that angles are accurately represented, which is crucial for determining bearings and navigating effectively. This allows for accurate plotting of courses and the determination of distances.
Q: Are conformal projections perfect?
A: No, all map projections introduce some distortion. Conformal projections prioritize angle accuracy, but they can still distort areas. The level of distortion varies depending on the projection and the region being mapped.
Tips for Understanding Conformal Projections
-
Visualize the projection process: Imagine the Earth being projected onto a surface, such as a cylinder, cone, or plane. This will help you understand how the projection distorts the Earth’s surface.
-
Compare different projections: Examine maps created using different projections and compare their distortions. This will highlight the strengths and weaknesses of each projection.
-
Consider the intended use: The choice of projection should be based on the specific application. For example, a conformal projection is ideal for navigation, while an equal-area projection is better for visualizing population density.
Conclusion
Conformal map projections are essential tools for accurately representing the Earth’s surface on a flat map. By preserving angles, they ensure that shapes are true to their real-world counterparts. While they do distort areas, their ability to maintain angular relationships makes them invaluable for navigation, meteorology, and other applications where precise angular measurements are paramount. Understanding the strengths and weaknesses of different conformal projections allows for informed decisions and the creation of maps that effectively communicate geographic information.

![]()

Closure
Thus, we hope this article has provided valuable insights into Conformal Map Projections: Preserving Shapes and Angles in a Flattened World. We thank you for taking the time to read this article. See you in our next article!